Physics Notes Form 3

Physics Notes Form 3 - Free KCSE Past Papers - Physics - Free KCSE Mocks - KCSE Questions and Answers - Download Free KCSE Marking Schemes - KCSE Revision - KCSE Results

Physics Notes Form 3
Physics Form Three
Chapter One
Linear Motion

Introduction

Study of motion is divided into two;

1. Kinematics

2. Dynamics

In kinematics forces causing motion are disregarded while dynamics deals with motion of objects and the forces causing them.

I. Displacement

Distance moved by a body in a specified direction is called displacement. It is denoted by letter‘s’ and has both magnitude and direction. Distance is the movement from one point to another. The Si unit for displacement is the metre (m).

II. Speed

This is the distance covered per unit time.

Speed= distance covered/ time taken. Distance is a scalar quantity since it has magnitude only.

The SI unit for speed is metres per second(m/s or ms^-1)

Average speed= total distance covered/total time taken Other units for speed used are Km/h.

Examples

1. A body covers a distance of 10m in 4 seconds. It rests for 10 seconds and finally covers a distance of 90m in 60 seconds. Calculate the average speed.

Solution

Total distance covered =10+90= 100m

Total time taken =4+10+6= 20 seconds

Therefore average speed = 100/20= 5m/s

2. Calculate the distance in metres covered by a body moving with a uniform speed of 180 km/h in 30 seconds.

Solution

Distance covered=speed*time

=180*1000/60*60=50m/s

=50*30

=1,500m

3. Calculate the time in seconds taken a by body moving with a uniform speed of 360km/h to cover a distance of 3,000 km?

Solution

Speed:360km/h=360*1000/60*60=100m/s

Time=distance/speed

3000*1000/100

=30,000 seconds.

III. Velocity

This is the change of displacement per unit time. It is a vector quantity.

Velocity=change in displacement/total time taken

The SI units for velocity are m/s

Examples

1. A man runs 800m due North in 100 seconds, followed by 400m due South in 80 seconds. Calculate,

a. His average speed

b. His average velocity

c. His change in velocity for the whole journey

Solution

a. Average speed: total distance travelled/total time taken

=800+400/100+80

=1200/180

=6.67m/s

b. Average velocity: total displacement/total time

=800-400/180

=400/180

=2.22 m/s due North

c. Change in velocity=final-initial velocity

= (800/100)-(400-80)

=8-5

=3m/s due North

2. A tennis ball hits a vertical wall at a velocity of 10m/s and bounces off at the same velocity. Determine the change in velocity.

Solution

Initial velocity(u)=-10m/s

Final velocity (v) = 10m/s

Therefore change in velocity= v-u

=10- (-10)

=20m/s

IV. Acceleration

This is the change of velocity per unit time. It is a vector quantity symbolized by ‘a’. Acceleration ‘a’=change in velocity/time taken= v-u/t The SI units for acceleration are m/s2 Examples 1. The velocity of a body increases from 72 km/h to 144 km/h in 10 seconds.

Calculate its acceleration.

Solution

Initial velocity= 72 km/h=20m/s

Final velocity= 144 km/h=40m/s

Therefore ‘a’ =v-u/t

= 40-20/10

2m/s2

2. A car is brought to rest from 180km/h in 20 seconds. What is its retardation?

Solution

Initial velocity=180km/h=50m/s

Final velocity= 0 m/s

A = v-u/t=0-50/20

= -2.5 m/s2

Hence retardation is 2.5 m/s2

Motion graphs

Distance-time graphs

Area under velocity-time graph

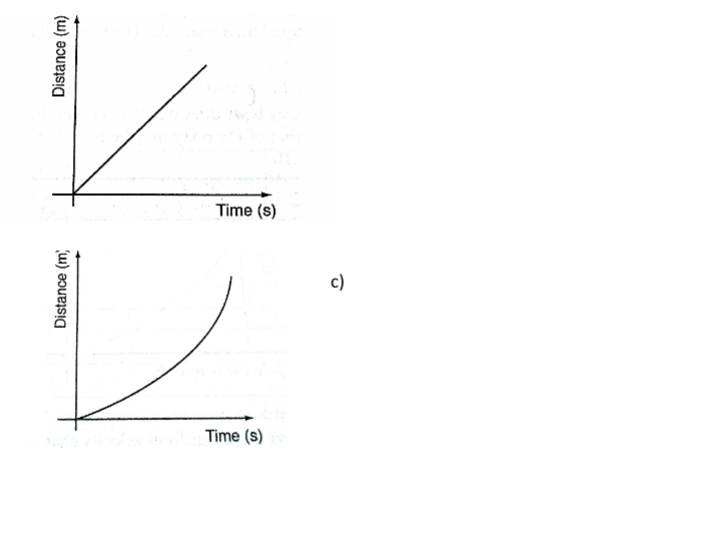
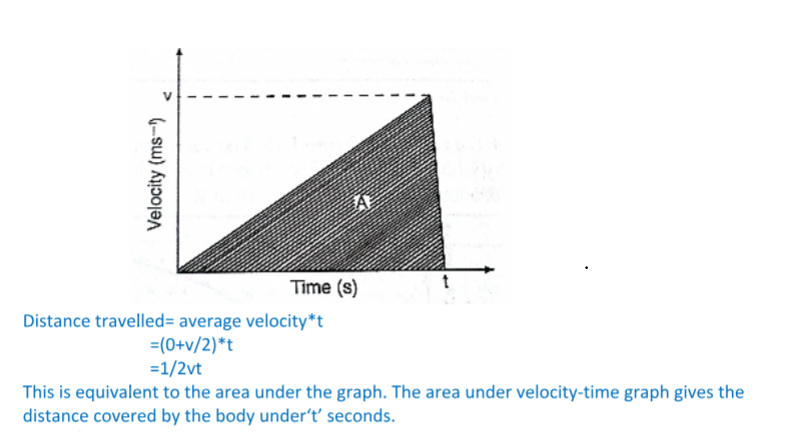
Consider a body with uniform or constant acceleration for time‘t’ seconds;

This is equivalent to the area under the graph. The area under velocity-time graph gives the distance covered by the body under‘t’ seconds.

Example

A car starts from rest and attains a velocity of 72km/h in 10 seconds.

It travels at this velocity for 5 seconds and then decelerates to stop after another 6 seconds.

Draw a velocity-time graph for this motion. From the graph;

i. Calculate the total distance moved by the car

ii. Find the acceleration of the car at each stage.

Solution

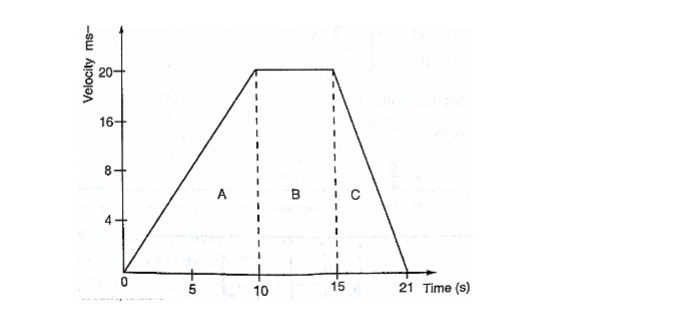
a. From the graph, total distance covered= area of (A+B+C)

=(1/2×10×20)+(1/2×6×20)+(5×20)

=100+60+100

=260m

Also the area of the trapezium gives the same result.

b. Acceleration= gradient of the graph

Stage A gradient= 20-0/ 10-0 = 2 m/s2

Stage b gradient= 20-20/15-10 =0 m/s2

Stage c gradient= 0-20/21-15 =-3.33 m/s2

Using a ticker-timer to measure speed, velocity and acceleration. It will be noted that the dots pulled at different velocities will be as follows;

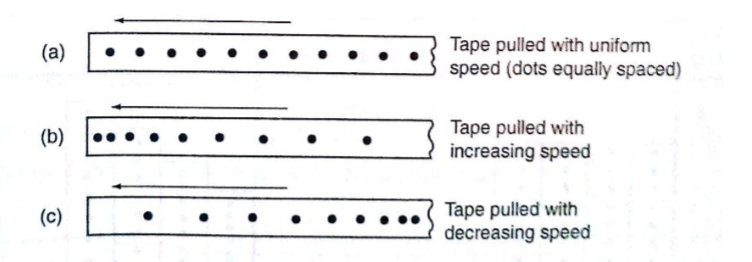
Most ticker-timers operate at a frequency of 50Hzi.e. 50 cycles per second hence they make 50 dots per second. Time interval between two consecutive dots is given as,

1/50 seconds= 0.02 seconds. This time is called a tick.

The distance is measured in ten-tick intervals hence time becomes 10×0.02= 0.2 seconds.

Examples

a. A tape is pulled steadily through a ticker-timer of frequency 50 Hz.

Given the outcome below, calculate the velocity with which the tape is pulled.

Solution

Distance between two consecutive dots= 5cm

Frequency of the ticker-timer=50Hz

Time taken between two consecutive dots=1/50=0.02 seconds

Therefore, velocity of tape=5/0.02= 250 cm/s

b. The tape below was produced by a ticker-timer with a frequency of 100Hz. Find the acceleration of the object which was pulling the tape.

Solution

Time between successive dots=1/100=0.01 seconds

Initial velocity (u) 0.5/0.01 50 cm/s

Final velocity (v) 2.5/0.01= 250 cm/s

Time taken= 4 ×0.01 = 0.04 seconds

Therefore, acceleration= v-u/t= 250-50/0.04=5,000 cm/s2

Equations of linear motion

The following equations are applied for uniformly accelerated motion;

v = u + at

s = ut + ½ at2

v2= u2 +2as

Examples

1. A body moving with uniform acceleration of 10 m/s2 covers a distance of 320 m. if its initial velocity was 60 m/s. Calculate its final velocity.

Solution

V2 = u2 +2as

= (60) +2×10×320

=3600+6400

= 10,000

Therefore v= (10,000)1/2

v= 100m/s

2. A body whose initial velocity is 30 m/s moves with a constant retardation of 3m/s. Calculate the time taken for the body to come to rest.

Solution

v = u+at

0= 30-3t

30=3t

t= 30 seconds.

3. A body is uniformly accelerated from rest to a final velocityof 100m/s in 10 seconds. Calculate the distance covered.

Solution

s=ut+ ½ at2

=0×10+ ½ ×10×102

= 1000/2=500m

Motion under gravity.

1. Free fall

The equations used for constant acceleration can be used to become,

v =u+gt

s =ut + ½ gt²

v2= u+2gs

2. Vertical projection

Since the body goes against force of gravity then the following equations hold

v =u-gt ……………1

s =ut- ½ gt2 ……2

v2= u-2gs …………3

N.B time taken to reach maximum height is given by the following

t=u/g since v=0 (using equation 1)

Time of flight

The time taken by the projectile is the timetaken to fall back to its point ofprojection. Using eq. 2 then, displacement =0

0= ut- ½ gt²

0=2ut-gt2

t(2u-gt)=0

Hence, t=0 or t= 2u/g

t=o corresponds to the start of projection

t=2u/gcorresponds to the time of flight

The time of flight is twice the time taken to attain maximum height.

Maximum height reached.

Using equation 3 maximum height, Hmax is attained when v=0 (final velocity).

Hence v2= u2-2gs;- 0=u2-2gHmax, therefore

2gHmax=u2

Hmax=u2/2g

Velocity to return to point of projection.

At the instance of returning to the original point, total displacement equals to zero.

v2 =u2-2gs hence v2= u2

Thereforev=u or v=±u

Example

A stone is projected vertically upwards with a velocity of 30m/s from the ground.

Calculate,

a. The time it takes to attain maximum height

b. The time of flight

c. The maximum height reached

d. The velocity with which it lands on the ground. (take g=10m/s)

Solution

a. Time taken to attain maximum height

T=u/g=30/10=3 seconds

b. The time of flight

T=2t= 2×3=6 seconds

Or T=2u/g=2×30/10=6 seconds.

c. Maximum height reached

Hmax= u2/2g= 30×30/2×10= 45m

d. Velocity of landing (return)

v2= u2-2gs, but s=0,

Hence v2=u2

Thereforev=(30×30)1/2=30m/s

3. Horizontal projection

The path followed by a body (projectile) is called trajectory.

The maximum horizontal distance covered by the projectile is called range.

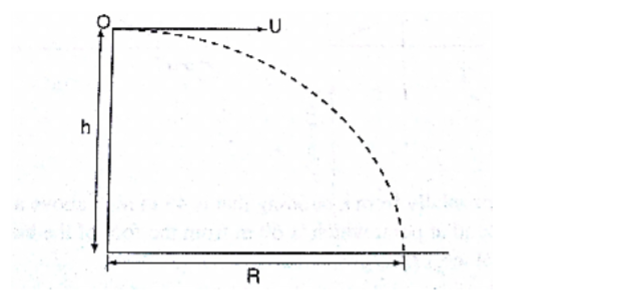
The horizontal displacement ‘R’ at a time‘t’ is given by s=ut+1/2at2 Taking u=u and a=0 hence R=ut, is the horizontal displacement and h=1/2gt2 is the vertical displacement.

NOTE

The time of flight is the same as the time of free fall.

Example

A ball is thrown from the top of a cliff 20m high with a horizontal velocity of 10m/s.

Calculate,

a. The time taken by the ball to strike the ground

b. The distance from the foot of the cliff to where the ball strikes the ground.

c. The vertical velocity at the time it strikes the ground. (take g=10m/s)

Solution

a. h= ½ gt2

20= ½ ×10×t2

40=10t2

t2=40/10=4

t=2 seconds

b. R=ut

=10×2

=20m

c. v=u+at=gt

= 2×10=20m/s

Chapter Two

Refraction of Light

Introduction

Refraction is the change of direction of light rays as they pass at an angle from one medium to another of different optical densities.

Exp. To investigate the path of light through rectangular glass block.

Apparatus: - soft-board, white sheet of paper, drawing pins (optical), rectangular glass block.

Procedure

1. Fix the white plain paper on the soft board using pins.

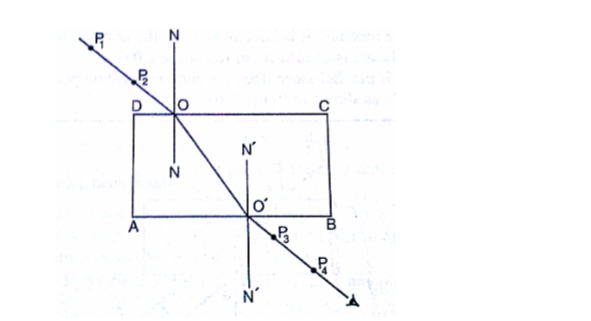
2. Place the glass block on the paper and trace its outline, label it ABCD as shown below.

3. Draw a normal NON at point O.

4. Replace the glass block to its original position.

5. Stick two pins P1 and P2 on the line such that they are at least 6cm apart and upright.

6. Viewing pins P1 and P2 from opposite side, fixpins P3 and P4 such that they’re in a straight line.

7. Remove the pins and the glass block.

8. Draw a line joining P3 and P4 and produce it to meet the outline face AB at point O

Explanation of refraction.

Light travels at a velocity of 3.0×108in a vacuum. Light travels with different velocities in different media. When a ray of light travels from an optically less dense media to more dense media, it is refracted towards the normal.

The glass block experiment gives rise to a very important law known as the law of reversibility which states that “if a ray of light is reversed, it always travels along its original path”.

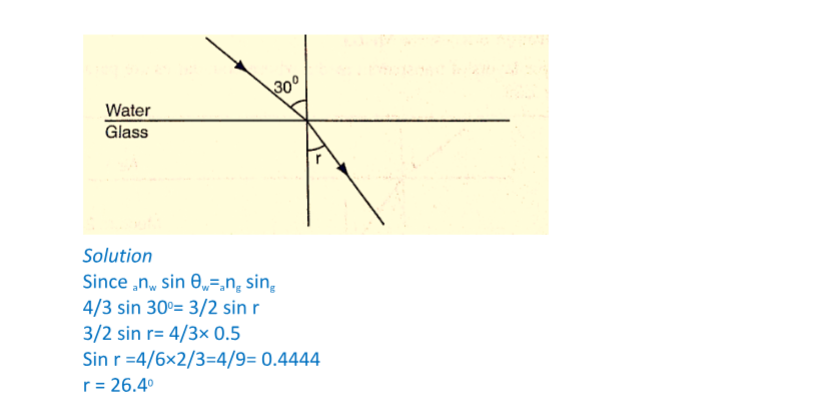
If the glass block is parallel-sided, the emergent ray will be parallel to the incident ray but displaced laterally as shown

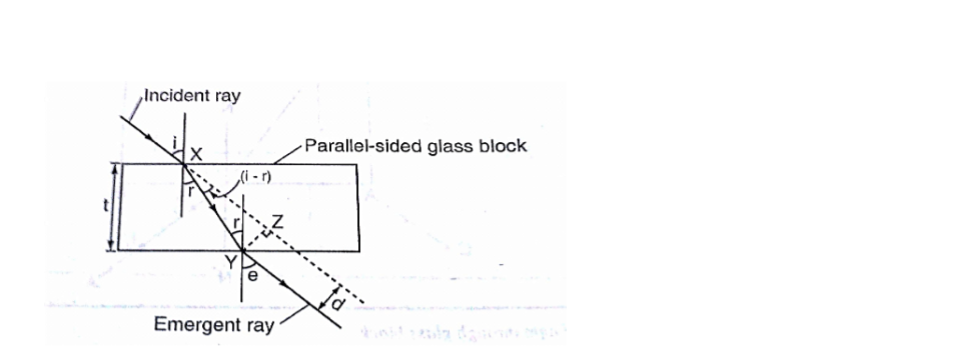
‘e’ is called the angle of emergence. The direction of the light is not altered but displaced sideways. This displacement is called lateral displacement and is denoted by‘d’.

Therefore XY= t/Cos r YZ= Sin (i-r) ×xy

So, lateral displacement, d = t Sin (i-r)/Cos r

Laws of refraction

1. The incident ray, the refracted ray and the normal at the point of incidence all lie on the same plane.

2. The ratio of the sine of the angle of incidence to the sine of the angle of refraction is a constant for a given pair of media.

Sin i/sin r = constant (k)

Refractive index

Refractive index (n) is the constant of proportionality in Snell’s law; hence

Sin i/ sin r = n

Therefore sin i/sin r=n=1/sin r/sin i

Examples

1. Calculate the refractive index for light travelling from glass to air given thatang= 1.5

Solution

gna= 1/ang = 1/1.5=0.67

2. Calculate the angle of refraction for a ray of light from air striking an air-glass interface, making an angle of 600 with the interface. (ang= 1.5)

Solution

Angle of incidence (i) = 900-600=300

1.5=sin 30^o/sin r, sin r =sin 300/ 1.5=0.5/1.5

Sin r=0.3333, sin-10.3333= 19.50

R= 19.50

Refractive index in terms of velocity.

Refractive index can be given in terms of velocity by the use of the following equation;

1n2 = velocity of light in medium 1/velocity of light in medium 2

When a ray of light is travelling from vacuum to a medium the refractive index is referred to as absolute refractive index of the medium denoted by ‘n’

Refractive index of a material ‘n’=velocity of light in a vacuum/velocity of light in material ‘n’

The absolute refractive indices of some common materials is given below

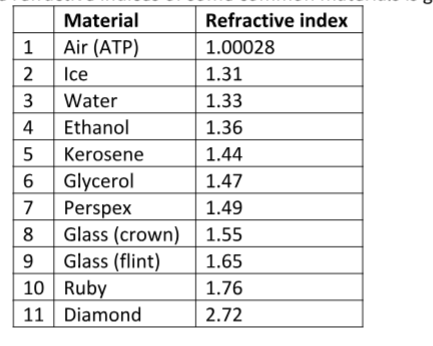
Examples 1. A ray of light is incident on a water-glass interface as shown. Calculate ‘r’. (Take the refractive index of glass and water as 3/2 and 4/3 respectively)

2. The refractive index of water is 4/3 and that of glass is 3/2. Calculate the refractive index of glass with respect to water.

Solution

wng= gna×ang, but wna = 1/ anw=3/4

wng=3/4×3/2=9/8= 1.13

Real and apparent depth

Consider the following diagram

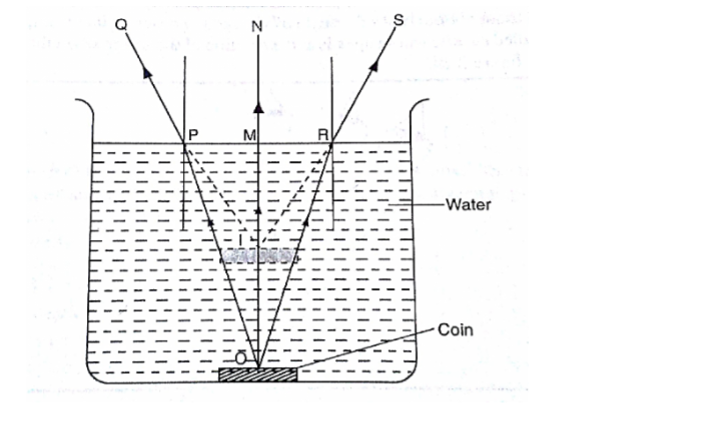
The depth of the water OM is the real depth, and the distance IM is known as the apparent depth. OI is the distance through which the coin has been displaced and is known as the vertical displacement.

The relationship between refractive index and the apparent depth is given by;

Refractive index of a material=real depth/apparent depth

This is true only if the object is viewed normally.

Example

A glass block of thickness 12 cm is placed on a mark drawn on a plain paper.

The mark is viewed normally through the glass. Calculate the apparent depth of the mark and hence the vertical displacement. (Refractive index of glass =3/2)

Solution

ang= real depth/apparent depth

apparent depth= real depth/ ang=(12×2)/3= 8 cm

vertical displacement= 12-8=4 cm

Applications of refractive index

Total internal reflection

This occurs when light travels from a denser optical medium to a less dense medium. The refracted ray moves away from the normal until a critical angle is reached usually 900 where the refracted ray is parallel to the boundary between the two media.

If this critical angle is exceeded total internal reflection occurs and at this point no refraction occurs but the ray is reflected internally within the denser medium.

Relationship between the critical angle and refractive index.

Consider the following diagram

From Snell’s law

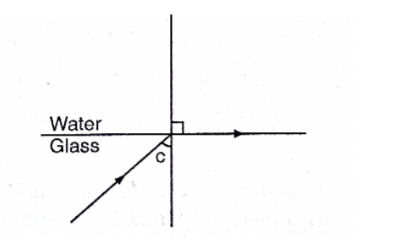
gnw = sin C/sin 900,but ang = 1/gna since sin 900 = 1

Thereforeang= 1/sin C, hence sin C=1/n or n=1/sin C

Example

Calculate the critical angle of diamond given that its refractive index is 2.42

Solution

Sin C= 1/n=1/ 2.42= 0.4132= 24.40

Effects of total internal reflection

1. Mirage: These are ‘pools of water’ seen on a tarmac road during a hot day.

They are also observed in very cold regions but the light curves in opposite direction such that a polar bear seems to be upside down in the sky.

2. Atmospheric refraction: the earths’ atmosphere refracts light rays so that the sun can be seen even when it has set. Similarly the sun is seen before it actually rises.

Applications of total internal reflection

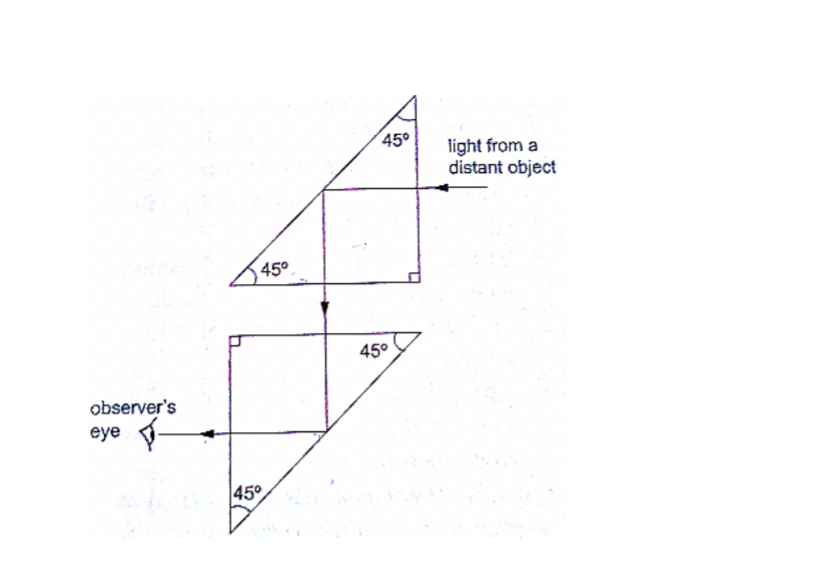
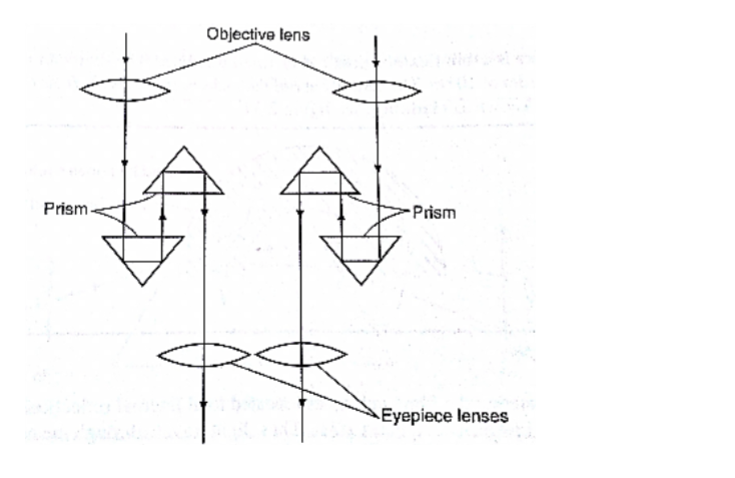
1. Periscope: a prism periscope consists of two right angled glass prisms of angles 450,900 and 450 arranged as shown below. They are used to observe distant objects.

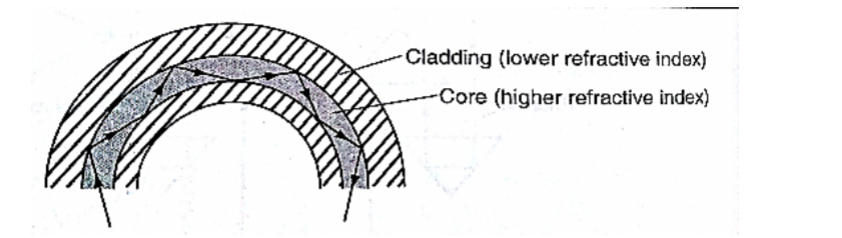
2. Prism binoculars: the arrangement of lenses and prisms is as shown below. Binoculars reduce the distance of objects such that they seem to be nearer.

3. Pentaprism: used in cameras to change the inverted images formed into erect and actual image in front of the photographer.

4. Optical fibre: this is a flexible glass rod of small diameter. A light entering through them undergoes repeated internal reflections.

They are used in medicine to observe or view internal organs of the body

5. Dispersion of white light:

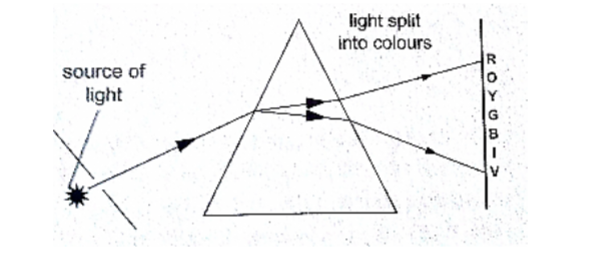
the splitting of light into its constituent colours is known as dispersion. Each colour represents a different wavelength as they strike the prism and therefore refracted differently as shown.

Chapter Three
Newton’s Laws of Motion

Newton’s first law (law of inertia)

This law states that “A body continues in its state of rest or uniform motion unless an unbalanced force acts on it”.

The mass of a body is a measure of its inertia. Inertia is the property that keeps an object in its state of motion and resists any efforts to change it.

Newton’s second law (law of momentum)

Momentum of a body is defined as the product of its mass and its velocity.

Momentum ‘p’=mv. The SI unit for momentum is kgm/s or Ns.

The Newton’s second law states that “The rate of change of momentum of a body is proportional to the applied force and takes place in the direction in which the force acts”

Change in momentum= mv-mu

Rate of change of momentum= mv-mu/∆t

Generally the second law gives rise to the equation of force F=ma

Hence F=mv-mu/∆t and F∆t=mv-mu

The quantity F∆t is called impulse and is equal to the change of momentum of the body. The SI unit for impulse is Ns.

Examples

1. A van of mass 3 metric tons is travelling at a velocity of 72 km/h. Calculate the momentum of the vehicle.

Solution

Momentum=mv=72km/h=(20m/s)×3×103 kg

=6.0×104kgm/s

2. A truck weighs 1.0×105 N and is free to move. What force willgiveit an acceleration of 1.5 m/s2? (take g=10N/kg)

Solution

Mass of the truck = (1.0×105)/10=6.0×104

Using F=ma

=1.5×10×104

=1.5×104 N

3. A car of mass 1,200 kg travelling at 45 m/s is brought to rest in 9 seconds.

Calculate the average retardation of the car and the average force applied by the brakes.

Solution

Since the car comes to rest, v=0, a=(v-u)/t =(0-45)/9=-5m/s (retardation)

F=ma =(1200×-5) N =-6,000 N (braking force)

4. A truck of mass 2,000 kg starts from rest on horizontal rails. Find the speed 3 seconds after starting if the tractive force by the engine is 1,000 N.

Solution

Impulse = Ft=1,000×3= 3,000 Ns

Let v be the velocity after 3 seconds.

Since the truck was initially at rest then u=0. Change in momentum=mv-mu

= (2,000×v) - (2,000×0)

=2,000 v

But impulse=change in momentum

2,000 v = 3,000

v = 3/2=1.5 m/s.

Weight of a body in a lift or elevator

When a body is in a lift at rest then the weight

W=mg

When the lift moves upwards with acceleration ‘a’ then the weight becomes

W = m (a+g)

If the lift moves downwards with acceleration ‘a’ then the weight becomes

W = m (g-a)

Example

A girl of mass stands inside a lift which is accelerated upwards at a rate of 2 m/s². Determine the reaction of the lift at the girls’ feet.

Solution

Let the reaction at the girls’ feet be ‘R’ and the weight ‘W’

The resultant force F= R-W

= (R-500) N

Using F = ma, then R-500= 50×2, R= 100+500 = 600 N.

Newton’s third law (law of interaction)

This law states that “For every action or force there is an equal and opposite force or reaction”

Example

A girl of mass 50 Kg stands on roller skates near a wall. She pushes herself against the wall with a force of 30N.

If the ground is horizontal and the friction on the roller skates is negligible, determine her acceleration from the wall.

Solution

Action = reaction = 30 N

Force of acceleration from the wall = 30 N

F = ma

a = F/m = 30/50 = 0.6 m/s2

Linear collisions

Linear collision occurs when two bodies collide head-on and move along the same straight line.

There are two types of collisions;

a) Inelastic collision: - this occurs when two bodies collide and stick together i.e. hitting putty on a wall. Momentum is conserved.

b) Elastic collision: - occurs when bodies collide and bounce off each other after collision. Both momentum and kinetic energy are conserved.

Collisions bring about a law derived from both Newton’s third law and conservation of momentum.

This law is known as the law of conservation of linear momentum which states that “when no outside forces act on a system of moving objects, the total momentum of the system stays constant”.

Examples

1. A bullet of mass 0.005 kg is fired from a gun of mass 0.5 kg.

If the muzzle velocity of the bullet is 300 m/s, determine the recoil velocity of the gun.

Solution

Initial momentum of the bullet and the gun is zero since they are at rest.

Momentum of the bullet after firing = (0.005×350) = 1.75 kgm/s

But momentum before firing = momentum after firing hence

0 = 1.75 + 0.5 v where ‘v’ = recoil velocity

0.5 v = -1.75

v =-1.75/0.5 = - 3.5 m/s (recoil velocity)

2. A resultant force of 12 N acts on a body of mass 2 kg for 10 seconds.

What is the change in momentum of the body?

Solution

Change in momentum = ∆P = mv – mu= Ft

= 12×10 = 12 Ns

3. A minibus of mass 1,500 kg travelling at a constant velocity of 72 km/h collides head-on with a stationary car of mass 900 kg.

The impact takes 2 seconds before the two move together at a constant velocity for 20 seconds.

Calculate

a) The common velocity

b) The distance moved after the impact

c) The impulsive force

d) The change in kinetic energy

Solution

a) Let the common velocity be ‘v’

Momentum before collision = momentum after collision

(1500×20) + (900×0) = (1500 +900)v

30,000 = 2,400v

v = 30,000/2,400 = 12.5 m/s (common velocity)

b) After impact, the two bodies move together as one with a velocity of 12.5 m/s

Distance = velocity × time

= 12.5×20

= 250m

c) Impulse = change in momentum

= 1500 (20-12.5) for minibus or

=900 (12.5 – 0) for the car

= 11,250 Ns

Impulse force F = impulse/time = 11,250/2 = 5,625 N

d) K.E before collision = ½ × 1,500 × 202 = 3 × 105 J

K.E after collision = ½ × 2400 × 12.52 = 1.875×105 J

Therefore, change in K.E =(3.00 – 1.875) × 105 = 1.25× 105 J

Some of the applications of the law of conservation of momentum

1. Rocket and jet propulsion: - rocket propels itself forward by forcing out its exhaust gases.

The hot gases are pushed through exhaust nozzle at high velocity therefore gaining momentum to move forward.

2. The garden sprinkler: - as water passes through the nozzle at high pressure it forces the sprinkler to rotate.

Solid friction

Friction is a force which opposes or tends to oppose the relative motion of two surfaces in contact with each other.

Measuring frictional forces

We can relate weight of bodies in contact and the force between them.

This relationship is called coefficient of friction.

Coefficient of friction is defined as the ratio of the force needed to overcome friction Ff to the perpendicular force between the surfaces Fn.

Hence µ = Ff/ Fn

Examples

1. A box of mass 50 kg is dragged on a horizontal floor by means of a rope tied to its front.

If the coefficient of kinetic friction between the floor and the box is 0.30, what is the force required to move the box at uniform speed?

Solution

Ff = µFn

Fn= weight = 50×10 = 500 N

Ff = 0.30 × 500 = 150 N

2. A block of metal with a mass of 20 kg requires a horizontal force of 50 N to pull it with uniform velocity along a horizontal surface.

Calculate the coefficient of friction between the surface and the block. (take g = 10 m/s)

Solution

Since motion is uniform, the applied force is equal to the frictional force

Fn = normal reaction = weight = 20 ×10 = 200 N

Therefore, µ =Ff/ Fn = 50/ 200 = 0.25.

Laws of friction

It is difficult to perform experiments involving friction and thus the following statements should therefore be taken merely as approximate descriptions:

1. Friction is always parallel to the contact surface and in the opposite direction to the force tending to produce or producing motion.

2. Friction depends on the nature of the surfaces and materials in contact with each other.

3. Sliding (kinetic) friction is less than static friction (friction before the body starts to slide).

4. Kinetic friction is independent of speed.

5. Friction is independent of the area of contact.

6. Friction is proportional to the force pressing the two surfaces together.

Applications of friction

1. Match stick

2. Chewing food

3. Brakes

4. Motion of motor vehicles

5. Walking

Methods of reducing friction

1. Rollers

2. Ball bearings in vehicles and machines

3. Lubrication / oiling

4. Air cushioning in hovercrafts

Example

A wooden box of mass 30 kg rests on a rough floor. The coefficient of friction between the floor and the box is 0.6. Calculate

a) The force required to just move the box

b) If a force of 200 N is applied the box with what acceleration will it move?

Solution

a) Frictional force Ff= µFn = µ(mg)

= 0.6×30×10 = 180 N

b) The resultant force = 200 – 180 = 20 N

From F =ma, then 20 = 30 a

a = 20 / 30 = 0.67 m/s²

Viscosity

This is the internal friction of a fluid. Viscosity of a liquid decreases as temperature increases.

When a body is released in a viscous fluid it accelerates at first then soon attains a steady velocity called terminal velocity.

Terminal velocity is attained when F + U = mg where F is viscous force, U is upthrust and mg is weight.

Chapter Four

Energy, Work, Power and Machines

Energy

This is the ability to do work.

Forms of energy.

1. Chemical energy: - this is found in foods, oils charcoal firewood etc.

2. Mechanical energy: - there are two types;

i. Potential energy – a body possesses potential energy due to its relative position or state

ii. Kinetic energy – energy possessed by a body due to its motion i.e. wind, water

iii. Wave energy – wave energy may be produced by vibrating objects or particles i.e. light, sound or tidal waves.

iv. Electrical energy – this is energy formed by conversion of other forms of energy i.e. generators.

Transformation and conservation of energy

Any device that facilitates energy transformations is called transducer. Energy can be transformed from one form to another i.e. mechanical – electrical – heat energy.

The law of conservation of energy states that “energy cannot be created or destroyed; it can only be transformed from one form to another”.

Work

Work is done when a force acts on a body and the body moves in the direction of the force.

Work done = force × distance moved by object

W = F × d

Work is measured in Nm. 1 Nm = 1 Joule (J)

Examples

1. Calculate the work done by a stone mason lifting a stone of mass 15 kg through a height of 2.0 m. (take g=10N/kg)

Solution

Work done = force × distance

= (15× 10) × 2 = 300 Nm or 300 J

2. A girl of mass 50 kg walks up a flight of 12 steps. If each step is 30 cm high, calculate the work done by the girl climbing the stairs.

Solution

Work done = force × distance

= (50× 10) × (12 ×30) ÷ 100 = 500 × 3.6 = 1,800 J

3. A force of 7.5 N stretches a certain spring by 5 cm. How much work is done in stretching this spring by 8.0 cm?

Solution

A force of 7.5 produces an extension of 5.0 cm.

Hence 8.0 cm = (7.5 ×8)/ 5 = 12.0 N

Work done = ½ × force × extension

= ½ × 12.0 × 0.08 = 0.48 J

4. A car travelling at a speed of 72 km/h is uniformly retarded by an applicationof brakes and comes to rest after 8 seconds. If the car with its occupants has a mass of 1,250 kg. Calculate;

a) The breaking force

b) The work done in bringing it to rest

Solution

a) F = ma and a = v – u/t

But 72 km/h = 20m/s

a = 0 -20/8 = - 2.5 m/s

Retardation = 2.5 m/s Braking force F = 1,250 × 2.5

= 3,125 N

b) Work done = kinetic energy lost by the car

= ½ mv2 – ½ mu2

= ½ × 1250 × 02 – ½ × 1250 × 202

= - 2.5 × 105 J

5. A spring constant k = 100 Nm is stretched to a distance of 20 cm. calculate the work done by the spring.

Solution

Work = ½ ks²

= ½ × 100 × 0.22

= 2 J

Power

Poweris the time rate of doing work or the rate of energy conversion.

Power (P)

= work done / time

P = W / t

The SI unit for power is the watt (W) or joules per second (J/s).

Examples

1. A person weighing 500 N takes 4 seconds to climb upstairs to a height of 3.0 m. what is the average power in climbing up the height?

Solution

Power = work done / time = (force × distance) / time

= (500 ×3) / 4 = 375 W

2. A box of mass 500 kg is dragged along a level ground at a speed of 12 m/s. If the force of friction between the box and floor is 1200 N. Calculate the power developed.

Solution

Power = F v

= 2,000 × 12

= 24,000 W = 24 kW.

Machines

A machine is any device that uses a force applied at one point to overcome a force at another point. Force applied is called the effort while the resisting force overcome is called load. Machines makes work easier or convenient to be done.

Three quantities dealing with machines are;-

a) Mechanical advantage (M.A.) - this is defined as the ratio of the load (L) to the effort (E). It has no units.

M.A = load (L) / effort (E)

b) Velocity ratio – this is the ratio of the distance moved by the effort to the distance moved by the load

V.R = distance moved by effort/ distance moved by the load

c) Efficiency – is obtained by dividing the work output by the work input and the getting percentage

Efficiency = (work output/work input) × 100

= (M.A / V.R) × 100

= (work done on load / work done on effort) × 100

Examples

1. A machine; the load moves 2 m when the effort moves 8 m. If an effort of 20 N is used to raise a load of 60 N, what is the efficiency of the machine?

Solution

Efficiency = (M.A / V.R) × 100 M.A = load/effort =60/20 = 3

V.R =DE/ DL = 8/2 = 4

Efficiency = ¾ × 100 = 75%

Some simple machines

a) Levers – this is a simple machine whose operation relies on the principle of moments

b) Pulleys – this is a wheel with a grooved rim used for lifting heavy loads to high levels. The can be used as a single fixed pulley, or as a block-and-tackle system.

Example

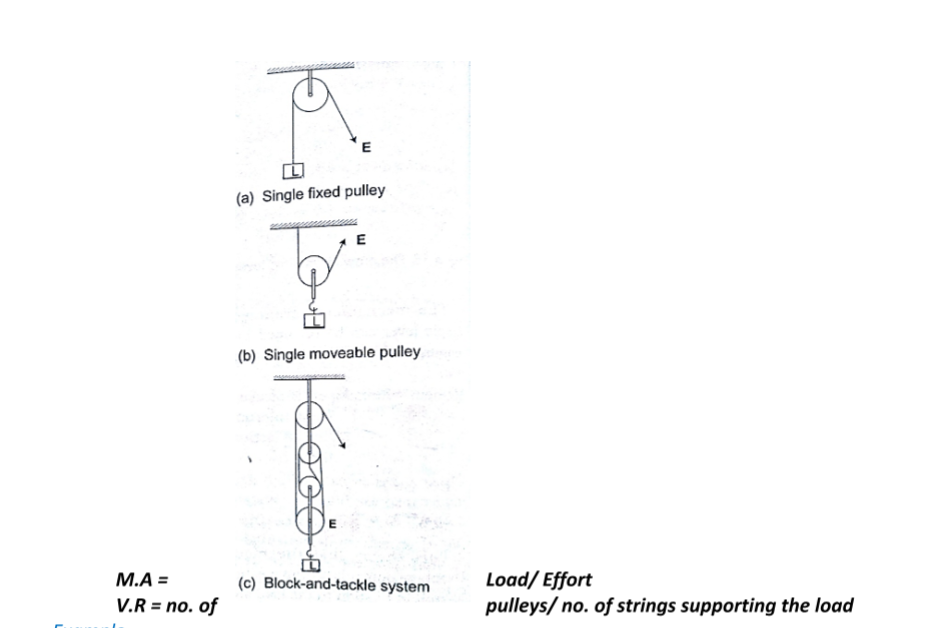
A block and tackle system has 3 pulleys in the upper fixed block and two in the lower moveable block. What load can be lifted by an effort of 200 N if the efficiency of the machine is 60%?

Solution

V.R = total number of pulleys = 5

Efficiency = (M.A /V.R) × 100 = 60%

0.6 = M.A/ 5 =3, but M.A = Load/Effort

Therefore, load = 3 ×200 = 600 N

c) Wheel and axle– consists of a large wheel of big radius attached to an axle of smaller radius.

Example

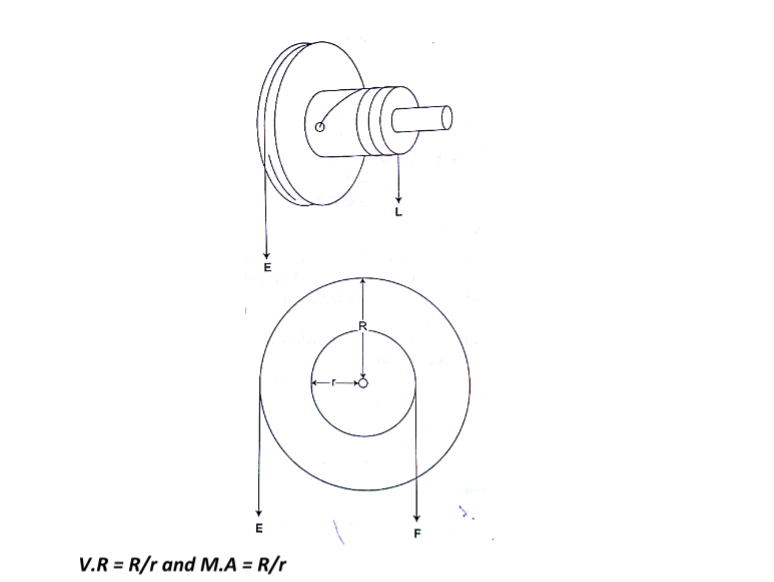
A wheel and axle is used to raise a load of 280 N by a force of 40 N applied to the rim of the wheel. If the radii of the wheel and axle are 70 cm and 5 cm respectively. Calculate the M.A, V.Rand efficiency.

Solution

M.A = 280 / 40 = 7

V.R = R/r = 70/5 = 14

Efficiency = (M.A/ V.R) × 100 = 7/14 × 100 = 50 %

d) Inclined plane:

V.R = 1/ sin θ M.A = Load/ Effort

Example

A man uses an inclined plane to lift a 50 kg load through a vertical height of 4.0 m.

the inclined plane makes an angle of 300 with the horizontal.

If the efficiency of the inclined plane is 72%, calculate;

a) The effort needed to move the load up the inclined plane at a constant velocity.

b) The work done against friction in raising the load through the height of 4.0 m. (take g= 10 N/kg)

Solution

a) V.R = 1 / sin C = 1/ sin 300 = 2 M.A = efficiency × V.R = (72/100)× 2 = 1.44

Effort = load (mg) / effort (50×10)/ 1.44 = 347.2 N

b) Work done against friction = work input – work output

Work output = mgh = 50×10×4 = 2,000 J

Work input = effort × distance moved by effort

347.2 × (4× sin 300) = 2,777.6 J

Therefore work done against friction = 2,777.6 – 2,000 = 777.6 J

e) The screw: - the distance between two successive threads is called the pitch V.R of screw = circumference of screw head / pitch P

= 2πr / P

Example

A car weighing 1,600 kg is lifted with a jack-screw of 11 mm pitch. If the handleis 28 cm from the screw, find the force applied.

Solution

Neglecting friction M.A = V.R

V.R = 2πr /P = M.A = L / E

1,600 / E = (2π× 0.28) / 0.011

E = (1,600 × 0.011 × 7) / 22×2×0.28 =10 N

f) Gears: - the wheel in which effort is applied is called the driver while the load wheel is the driven wheel.

V.R = revolutions of driver wheel / revolutions of driven wheel

V.R = no.of teeth in the driven wheel/ no. of teeth in the driving wheel

Example

g) Pulley belts: -these are used in bicycles and other industrial machines V.R = radius of the driven pulley / radius of the driving pulley

h) Hydraulic machines

V.R = R2 / r2 where R- radius of the load piston and r- radius of the effort piston

Example

The radius of the effort piston of a hydraulic lift is 1.4 cm while that of the load piston is 7.0 cm.

This machine is used to raise a load of 120 kg at a constant velocity through a height of 2.5 cm. given that the machine is 80% efficient, calculate;

a) The effort needed

b) The energy wasted using the machine

Solution

a) V.R = R2 / r2 = (7×7) / 1.4 × 1.4 = 25

Efficiency = M.A / V.R = (80 /100) × 25 = 20

But M.A = Load / Effort = (120×10) / 20 = 60 N

b) Efficiency = work output / work input = work done on load (m g h) /80

= (120 × 10× 2.5) / work input

80 / 100 = 3,000 / work input

Work input = (3,000 × 100) /80 = 3,750 J

Energy wasted = work input – work output

= 3,750 – 3,000 = 750 J

Chapter Five

Current Electricity

Electric potential difference and electric current

Electric current

Electric potential difference (p. d) is defined as the work done per unit charge in moving charge from one point to another. It is measured in volts.

Electric current is the rate of flow of charge. P. d is measured using a voltmeter while current is measured using an ammeter. The SI units for charge is amperes (A).

Ammeters and voltmeters

In a circuit an ammeter is always connected in series with the battery while a voltmeter is always connected parallel to the device whose voltage is being measured.

Ohm’s law

This law gives the relationship between the voltage across a conductor and the current flowing through it.

Ohm’s law states that “the current flowing through a metal conductor is directly proportional to the potential difference across the ends of the wire provided that temperature and other physical conditions remain constant”

Mathematically V α I

So V /I = constant, this constant of proportionality is called resistance

V / I = Resistance (R)

Resistance is measured in ohms and given the symbol Ω

Examples

1. A current of 2m A flows through a conductor of resistance 2 kΩ. Calculate the voltage across the conductor.

Solution

V = IR = (2 × 10-3) × (2 × 103) = 4 V.

2. A wire of resistance 20Ω is connected across a battery of 5 V. What current is flowing in the circuit?

Solution

I = V/R = 5 / 20 = 0.25 A

Ohmic and non-ohmic conductors

Ohmic conductors are those that obey Ohms law(V α I) and a good example is nichrome wire i.e. the nichrome wire is not affected by temperature.

Non-ohmic conductors do not obey Ohms law i.e. bulb filament (tungsten), thermistor couple, semi-conductor diode etc. They are affected by temperature hence non-linear.

Factors affecting the resistance of a metallic conductor

1. Temperature – resistance increases with increase in temperature

2. Length of the conductor– increase in length increases resistance

3. Cross-sectional area– resistance is inversely proportional to the cross-sectional area of a conductor of the same material.

Resistivity of a material is numerically equal to the resistance of a material of unit length and unit cross-sectional area. It is symbolized by ρ and the units are ohmmeter (Ωm).

It is given by the following formula;

ρ = AR /lwhere A – cross-sectional area, R – resistance, l – length

Example

Given that the resistivity of nichrome is 1.1× 10-6Ωm, what length of nichrome wire of diameter 0.42 mm is needed to make a resistance of 20 Ω?

Solution

ρ = AR /l, hence l = RA/ ρ = 20 × 3.142 × (2.1×10-4) / 1.1 × 10-6 = 2.52 m

Resistors

Resistors are used to regulate or control the magnitude of current and voltage in a circuit according to Ohms law.

Types of resistors

i) Fixed resistors – they are wire-wound or carbon resistors and are designed togive a fixed resistance.

ii) Variable resistors – they consist of the rheostat and potentiometer. The resistance can be varied by sliding a metal contact to generate desirable resistance.

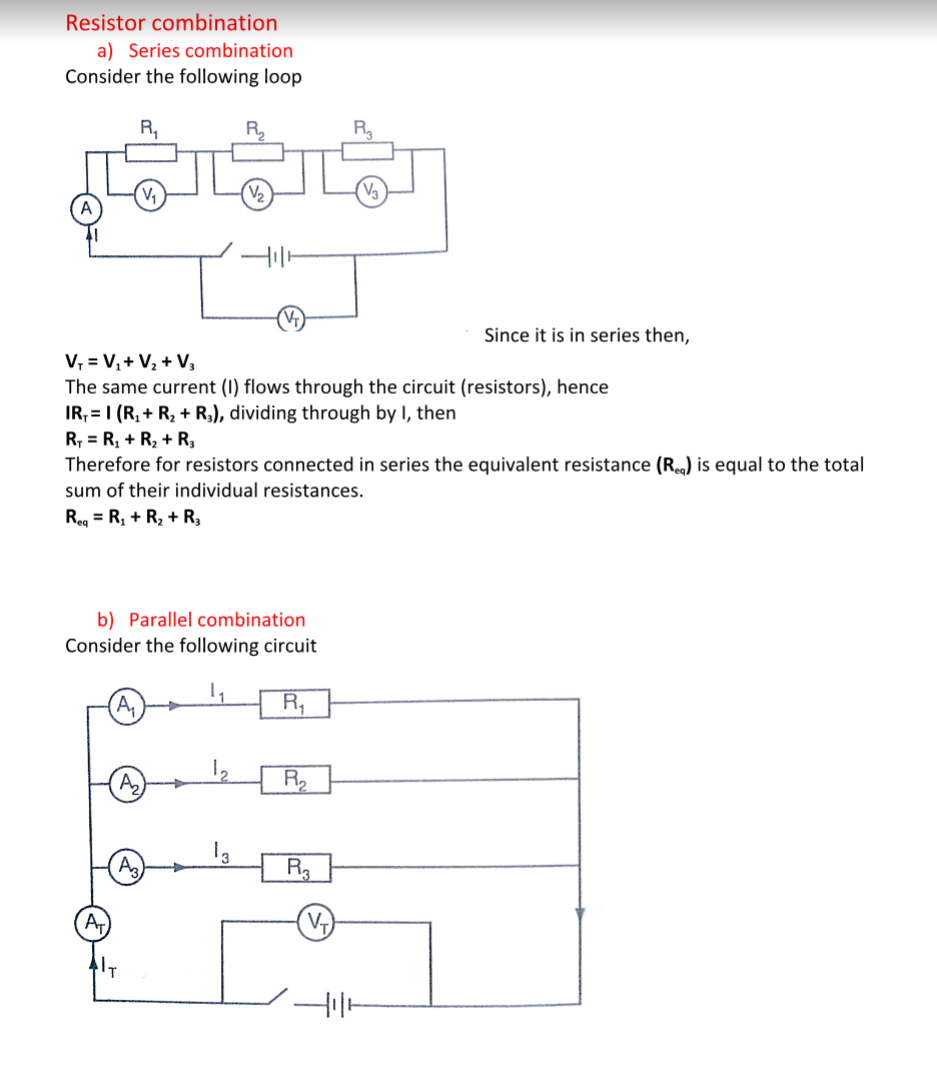
Resistor combination

a) Series combination

Consider the following loop

Combining those in series then this can be replaced by two resistors of 60 Ω and 40 Ω.

Current through 10 Ω = (p.d. between P and R)/ (30 + 10) Ω

p.d between P and R = 0.8 × Req. Req = (40 × 60)/ 40 + 60 = 2400/ 100 = 24 Ω

p.d across R and P = 0.8 × 24 (V=IR)

therefore, current through 10 Ω = 19.2 / 10 + 30 = 0.48 A

Electromotive force and internal resistance

Electromotive force (e.m.f.) is the p.d across a cell when no current is being drawn from the cell.

The p.d across the cell when the circuit is closed is referred to as the terminal voltage of the cell.

Internal resistance of a cell is therefore the resistance of flow of current that they generate. Consider the following diagram;

The current flowing through the circuit is given by the equation,

Current = e.m.f / total resistance

I = E / R + rwhere E – e.m.f of the cell

Therefore E = I (R + r) = IR + I r = V + I r

Examples

1. A cell drives a current of 0.6 A through a resistance of 2 Ω. if the value of resistance is increased to 7 Ω the current becomes 0.2 A.

calculate the value of e.m.f of the cell and its internal resistance.

Solution

Let the internal resistance be ‘r’ and e.m.f be ‘E’.

Using E = V + I r = IR + I r

Substitute for the two sets of values for I and R

E = 0.6 × (2 + 0.6 r) = 1.2 + 0.36 r

E = 0.6 × (7 × 0.2 r) = 1.4 + 0.12 r

Solving the two simultaneously, we have,

E = 1.5 v and R = 0.5 Ω

2. A battery consists of two identical cells, each of e.m.f 1.5 v and internal resistance of 0.6 Ω, connected in parallel. Calculate the current the battery drives through a 0.7 Ω resistor.

Solution

When two identical cells are connected in series, the equivalent e.m.f is equal to that of only one cell.

The equivalent internal resistance is equal to that of two such resistance connected in parallel.

Hence Req = R1 R2 / R1 + R2 = (0.6 × 0.6) / 0.6 + 0.6 = 0.36 / 1.2 = 0.3 Ω

Equivalent e.m.f =1.5 / (0.7 + 0.3) = 1.5 A

Hence current flowing through 0.7 Ω resistor is 1.5 A

Chapter Six

Waves II

Properties of waves

Waves exhibit various properties which can be conveniently demonstrated using the ripple tank.

It consists of a transparent tray filled with water and a white screen as the bottom. On top we have a source of light.

A small electric motor (vibrator) is connected to cause the disturbance which produces waves.

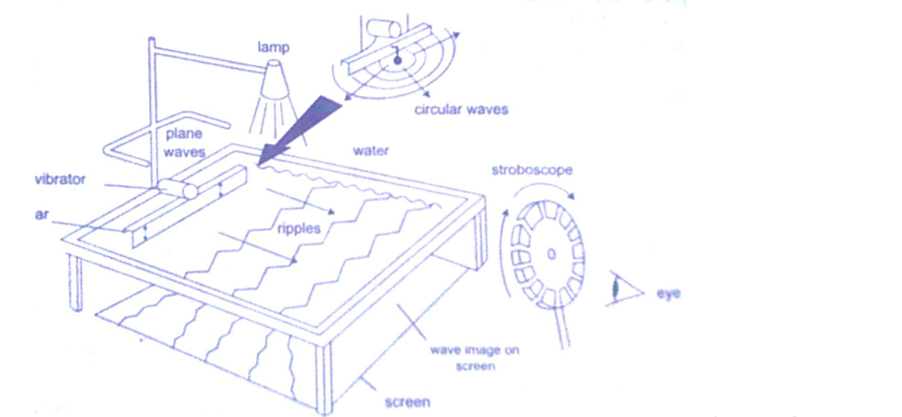
The wave fronts represent wave patterns as they move along.

Rectilinear propagation

This is the property of the waves travelling in straight lines and perpendicular to the wave front.

The following diagrams represent rectilinear propagation of water waves.

Refraction

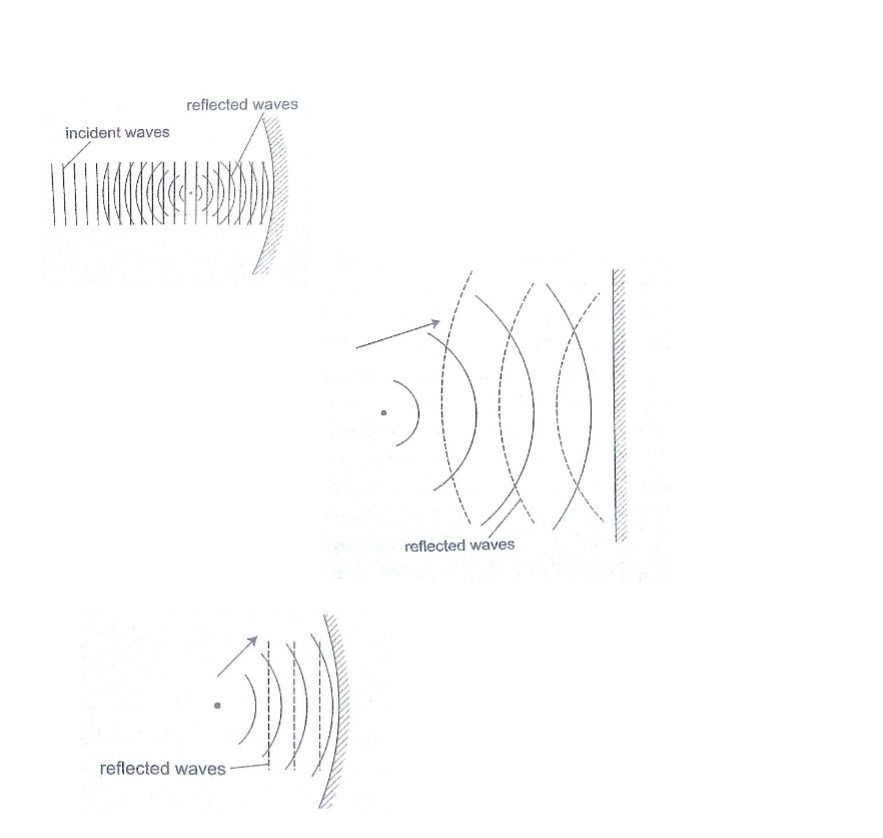
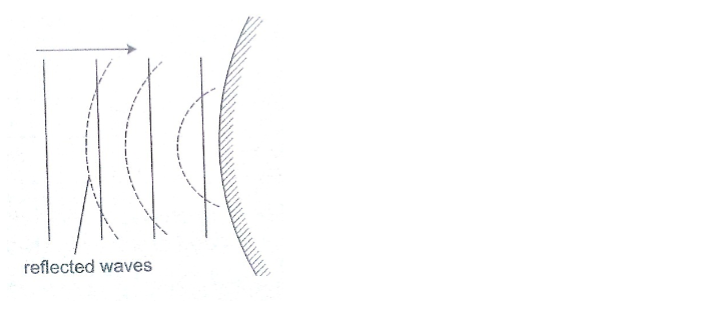
This is the change of direction of waves at a boundary when they move from one medium to another.

This occurs when an obstacle is placed in the path of the waves. The change of direction occurs at the boundary between deep and shallow waters and only when the waves hit the boundary at an angle.

Diffraction of waves

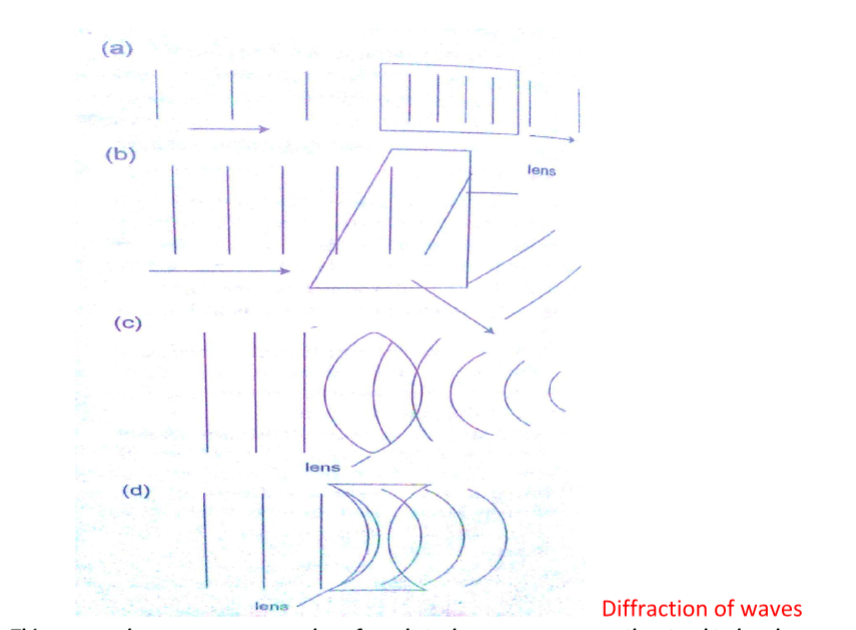
This occurs when waves pass an edge of an obstacle or a narrow gap, they tend to bend around the corner and spread out beyond the obstacle or gap.

Interference of waves

This occurs when two waves merge and the result can be a much larger wave, smaller wave or no wave at all.

When the waves are in phase they add up and reinforce each other. This is called a constructive interference and when out of phase they cancel each other out and this is known as destructive interference.

Interference in sound

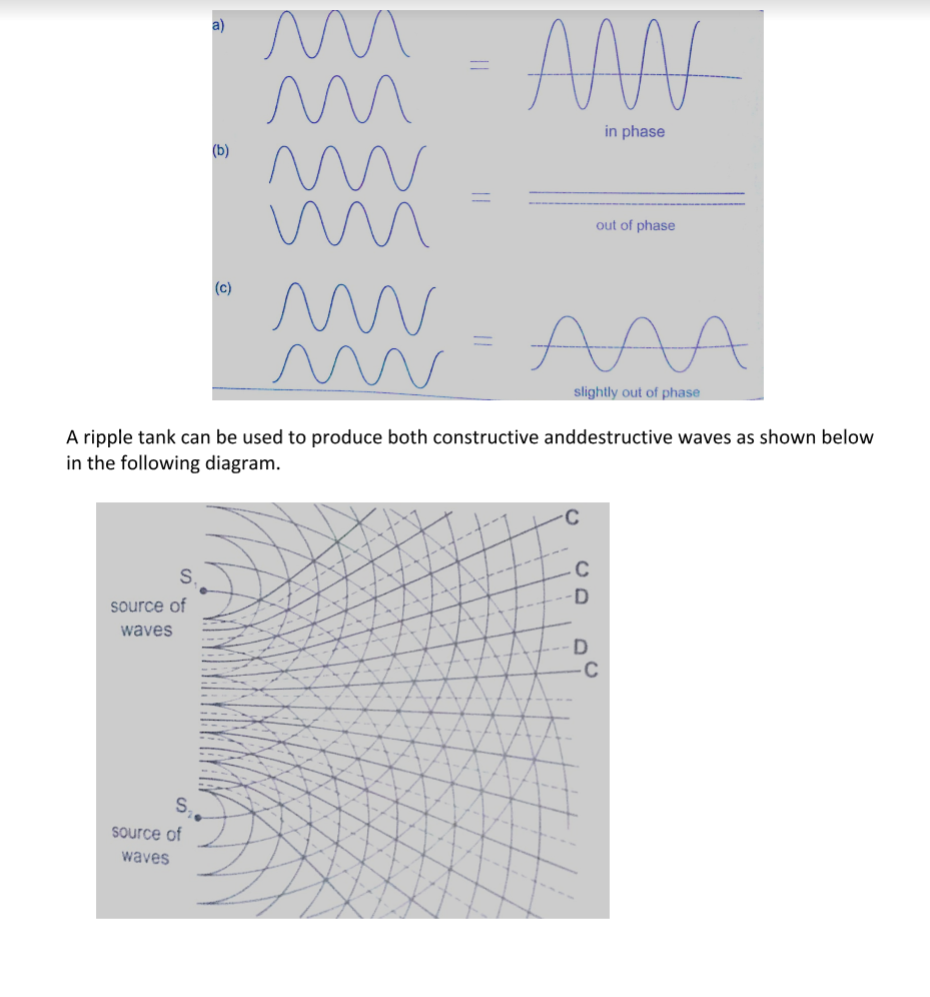
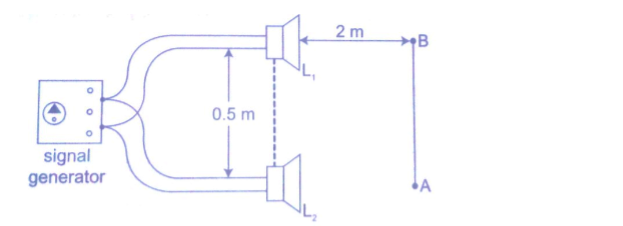
Two loud speakers L1 and L2 are connected to the same signal generator so that sound waves from each of them are in phase.

The two speakers are separated by a distance of the order of wavelengths i.e. 0.5 m apart for sound frequency of 1,000 Hz.

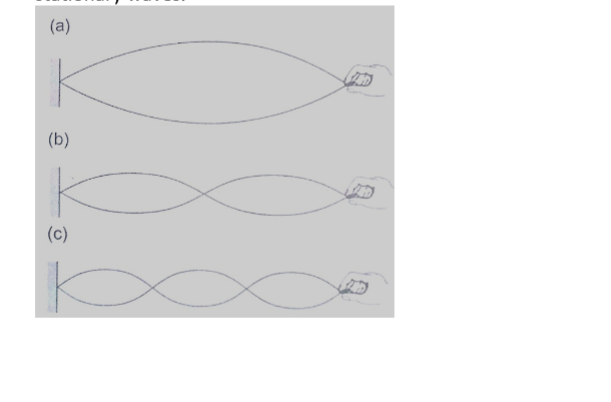
If you walk along line AB about 2m away from the speakers, the intensity of sound rises and falls alternately hence both destructive and constructive interference will be experienced.

Stationary waves

They are also known as standing waves and are formed when two equal progressive waves travelling in opposite direction are superposed on each other.

When the two speakers are placed facing each other they produce standing waves.

A rope tied at one end will still produce stationary waves.

Chapter Seven
Electrostatics II

Electric fields

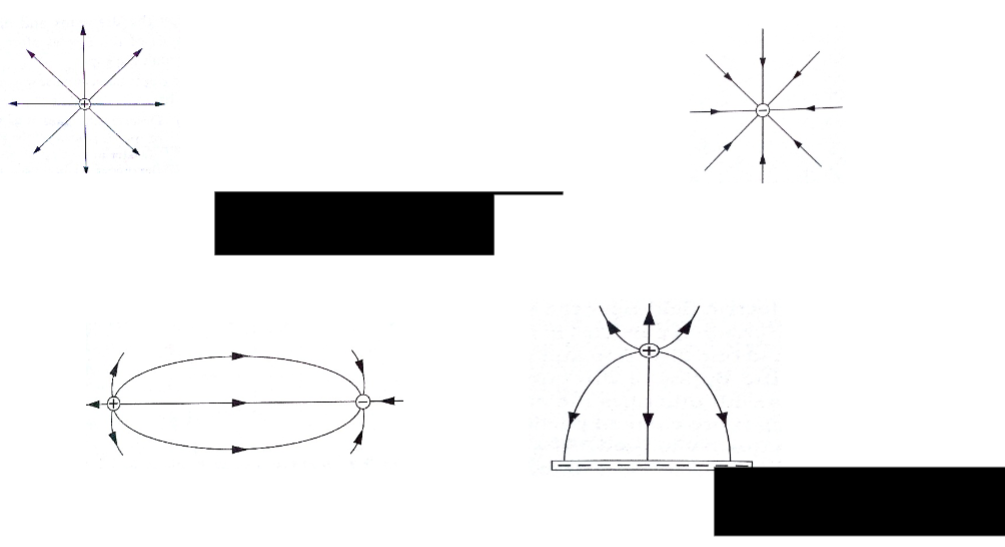
An electric field is the space around a charged body where another charged body would be acted on by a force. These fields are represented by lines of force.

This line of force also called an electric flux line points in the direction of the force.

Electric field patterns

Just like in magnetic fields, the closeness of the electric field-lines of force is the measure of the field strength.

Their direction is always from the north or positive to the south or negative.

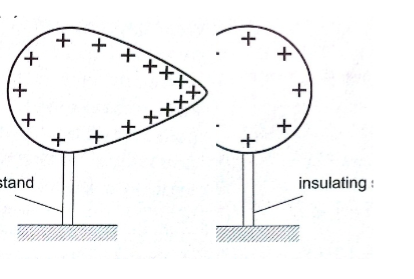
Charge distribution on conductors’ surface

A proof plane is used to determine charge distribution on spherical or pear-shaped conductors.

For an isolated sphere it is found that the effect is the same for all points on the surface meaning that the charge is evenly distributed on all points on the spherical surface.

For appear-shaped conductor the charge is found to be denser in the regions of large curvature (small radius).

The density of charge is greatest where curvature is greatest.

Charges on or action at sharp points

A moving mass of air forms a body with sharp points.

The loss of electrons by molecules (ionization) makes the molecules positively charged ions.

These ions tend to move in different directions and collide producing more charged particles and this makes the air highly ionized.

When two positively charged bodies are placed close to each other, the air around them may cause a spark discharge which is a rush of electrons across the ionized gap, producing heat, light and sound in the process which lasts for a short time.

Ionization at sharp projections of isolated charged bodies may sometimes be sufficient to cause a discharge.

This discharge produces a glow called corona discharge observed at night on masts of ships moving on oceans.

The same glow is observed on the trailing edges of aircrafts.

This glow in aircrafts and ships is called St. Elmo’s fire. Aircrafts are fitted with ‘pig tails’ on the wings to discharge easily.

The lightning arrestors

Lightning is a huge discharge where a large amount of charge rushes to meet the opposite charge.

It can occur between clouds or the cloud and the earth. Lightning may not be prevented but protection from its destruction may be done through arrestors.

An arrestor consists of a thick copper strip fixed to the outside wall of a building with sharp spikes.

Capacitors and capacitance

A capacitor is a device used for storing charge.

It consists of two or more plates separated by either a vacuum or air.

The insulating material is called ‘dielectric’. They are symbolized as shown below,

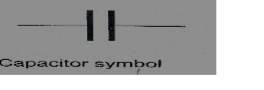
Capacitance C = Q / V where Q- charge and V – voltage.

The units for capacitance are coulombs per volt (Coul /volt) and are called farads.

1 Coul/ volt = 1 farad (F)

1 µF = 10-6 F and 1pF = 10-12

Types of capacitors are;

a) Paper capacitors

b) Electrolyte capacitors

c) Variable capacitors

d) Plastic capacitors

e) Ceramic capacitors

f) Mica capacitors

Factors affecting the capacitance of a parallel-plate capacitor

1. Distance between the plates: - reducing separation increases capacitance but the plates should not be very close to avoid ionization which may lead to discharge.

2. Area of plate: - reduction of the effective area leads to reduction in capacitance.

3. Dielectric material between plates: - different materials will produce different capacitance effects.

Charging and discharging a capacitor

When the switch S1 is closed the capacitor charges through resistor R and discharges through the same resistor when switch S2 is closed.

Applications of capacitors

1. Variable capacitor: - used in tuning radios to enable it transmit in different frequencies.

2. Paper capacitors: - used in mains supply and high voltage installations.

3. Electrolytic capacitors: - used in transistor circuits where large capacitance values are required.

Other capacitors are used in reducing sparking as a car is ignited, smoothing rectified current and increasing efficiency in a. c. power transmission.

Example

A capacitor of two parallel plates separated by air has a capacitance of 15pF.

A potential difference of 24 volts is applied across the plates,

a) Determine the charge on the capacitors.

b) When the space is filled with mica, the capacitance increases to 250pF.

How much more charge can be put on the capacitor using a 24 V supply?

Solution

: a) C= Q / V then Q = VC, hence Q = (1.5 × 10-12) × 24 = 3.6 × 10-10 Coul.

b) Mica C = 250pF, Q = (250 × 10-12) × 24 = 6 × 10-9 Coul.

Additional charge = (6 × 10-9) – (3.6 × 10-10) = 5.64 × 10-9 Coul.

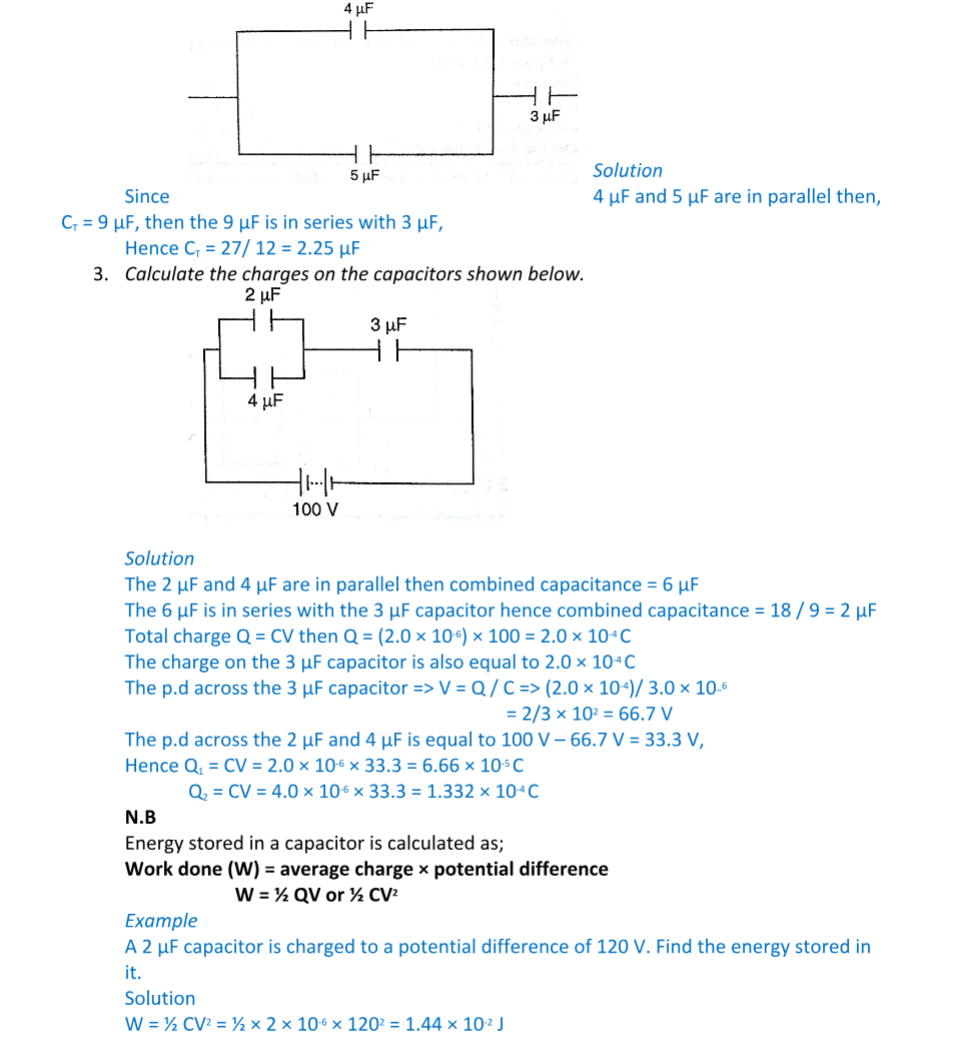
Capacitor combination

Chapter Eight

Heating Effect of an Electric Current

When current flows, electrical energy is transformed into other forms of energy i.e. light, mechanical and chemical changes.

Factors affecting electrical heating

Energy dissipated by current or work done as current flows depends on,

a) Current

b) Resistance

c) Time

This formula summarizes these factors as, E = I2 R t, E = I V t or E = V2 t / R

Examples

1. An iron box has a resistance coil of 30 Ω and takes a current of 10 A. Calculate the heat in kJ developed in 1 minute.

Solution

E = I2 R t = 102 × 30 × 60 = 18 × 104 = 180 kJ

2. A heating coil providing 3,600 J/min is required when the p.d across it is 24 V. Calculate the length of the wire making the coil given that its cross-sectional area is 1 × 10-7 m2 and resistivity 1 × 10-6 Ω m.

Solution

E = P t hence P = E / t = 3,600 / 60 = 60 W

P = V2 / R therefore R = (24 × 24)/ 60 = 9.6 Ω

R = ρ l/ A, l = (RA) / ρ = (9.6 × 1 × 10-7) / 1 × 10-6 = 0.96 m

Electrical energy and power

In summary, electrical power consumed by an electrical appliance is given by;

P = V I

P = I2 R

P = V2 / R

The SI unit for power is the watt (W)

1 W = 1 J/s and 1kW = 1,000 W.

Examples

1. What is the maximum number of 100 W bulbs which can be safely run from a 240 V source supplying a current of 5 A?

Solution

Let the maximum number of bulbs be ‘n’. Then 240 × 5 = 100 n

So ‘n’ = (240 × 5)/ 100 = 12 bulbs.

2. An electric light bulb has a filament of resistance 470 Ω.

The leads connecting the bulb to the 240 V mains have a total resistance of 10 Ω. Find the power dissipated in the bulb and in the leads.

Solution

Req = 470 + 10 = 480 Ω, therefore I = 240 / 480 = 0.5 A.

Hence power dissipated = I2 R = (0.5)2 × 470 = 117.5 W (bulb alone)

For the leads alone, R = 10 Ω and I = 0.5 A

Therefore power dissipated = (0.5)2 × 10 = 2.5 W.

Applications of heating of electrical current

1. Filament lamp – the filament is made up of tungsten, a metal with high melting point (3.400 0C). It is enclosed in aglass bulb with air removed and argon or nitrogen injected to avoid oxidation. This extends the life of the filament.

2. Fluorescent lamps – when the lamp is switched on, the mercury vapour emits ultra violet radiation making the powder in the tube fluoresce i.e. emit light. Different powders emit different colours.

3. Electrical heating – electrical fires, cookers e.tc. their elements are made up nichrome ( alloy of nickel and chromium) which is not oxidized easily when it turns red hot.

4. Fuse – this is a short length of wire of a material with low melting point (often thinned copper) which melts when current through it exceeds a certain value. They are used to avoid overloading.

Chapter Nine
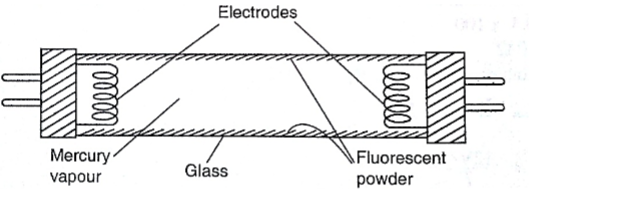
Quantity of Heat

Heat is a form of energy that flows from one body to another due to temperature differences between them.

Heat capacity

Heat capacity is defined as the quantity of heat required to raise the temperature of a given mass of a substance by one degree Celsius or one Kelvin. It is denoted by ‘C’.

Heat capacity, C = heat absorbed, Q / temperature change θ.

The units of heat capacity are J / 0C or J / K.

Specific heat capacity.

S.H.C of a substance is the quantity of heat required to raise the temperature of 1 kg of a substance by 1 0C or 1 K. It is denoted by ‘c’, hence,

c = Q / m θ where Q – quantity of heat, m – mass andθ – change in temperature.

The units for ‘c’ are J kg-1 K-1. Also Q = m c θ.

Examples

1. A block of metal of mass 1.5 kg which is suitably insulated is heated from 30 0C to 50 0C in 8 minutes and 20 seconds by an electric heater coil rated 54 watts.

Find;

a) The quantity of heat supplied by the heater

b) The heat capacity of the block

c) Its specific heat capacity

Solution

a) Quantity of heat = power × time = P t

= 54 × 500 = 27,000 J

b) Heat capacity, C = Q / θ = 27,000 / (50 – 30) = 1,350 J Kg-1 K^-1

c) Specific heat capacity, c = C / m = 1,350 / 1.5 = 900 J Kg^-1

2. If 300 g of paraffin is heated with an immersion heater rated 40 W, what is the temperature after 3 minutes if the initial temperature was 20 0C? (S.H.C for paraffin = 2,200 JK ^-1 K^-1). Solution

Energy = P t = m c θ = Q = quantity of heat.

P t = 40 × 180 = 7,200 J

m = 0.30 kg c = 2,200, θ = ..?

Q = m c θ, θ = Q / m c = 7,200 / (0.3 × 2,200) = 10.9 0C

3. A piece of copper of mass 60 g and specific heat capacity 390 J Kg-1 K-1 cools from 90 0C to 40 0C. Find the quantity of heat given out.

Solution

Q = m c θ, = 60 × 10-3 × 390 × 50 = 1,170 J.

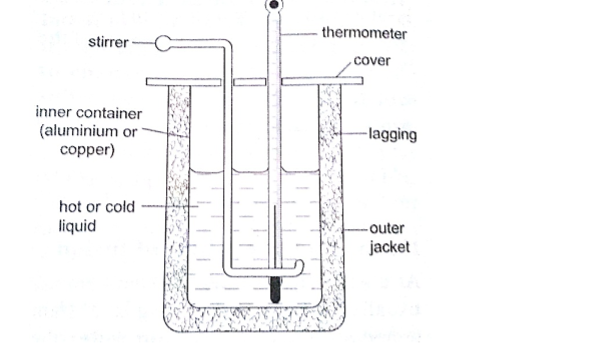
Determination of specific heat capacity

: A calorimeter is used to determine the specific heat capacity of a substance.

This uses the principle of heat gained by a substance is equal to the heat lost by another substance in contact with each other until equilibrium is achieved.

Heat losses in calorimeter are controlled such that no losses occur or they are very minimal.

Examples

1. A 50 W heating coil is immersed in a liquid contained in an insulated flask of negligible heat capacity.

If the mass of the liquid is 10 g and its temperature increases by 10 0C in 2 minutes, find the specific heat capacity of the liquid.

Solution

Heat delivered (P t) = 50 × 2 × 60 = 2,400 J

Heat gained = 0.1 × c × 10 J

Therefore ‘c’ = 2,400 / 0.1 × 10 = 2,400 J Kg^-1 K^-1 2. A metal cylinder mass 0.5 kg is heated electrically.

If the voltmeter reads 15V, the ammeter 0.3A and the temperatures of the block rises from 20 0C to 85 0C in ten minutes.

Calculate the specific heat capacity of the metal cylinder.

Solution

Heat gained = heat lost, V I t = m c θ

15 × 3 × 10 × 60 = 0.5 × c × 65

c = (15 × 3 × 600)/ 0.5 × 65 = 831 J Kg-1 K^-1

Fusion and latent heat of fusion

Fusion is the change of state from solid to liquid.

Change of state from liquid to solid is called solidification.

Latent heat of fusion is the heat energy absorbed or given out during fusion. Specific latent heat of fusion of a substance is the quantity of heat energy required to change completely 1 kg of a substance at its melting point into liquid without change in temperature.

It is represented by the symbol (L), we use the following formula, Q = m Lf

Different substances have different latent heat of fusion.

Factors affecting the melting point

a) Pressure

b) Dissolved substances

Specific latent heat of vaporization is the quantity of heat required to change completely 1 kg of a liquid at its normal boiling point to vapour without changing its temperature.

Hence

Q = m Lv

The SI unit for specific latent heat of vaporization is J / Kg.

Example

An immersion heater rated 600 W is placed in water. After the water starts to boil, the heater is left on for 6 minutes.

It is found that the mass of the water had reduced by 0.10 kg in that time.

Estimate the specific heat of vaporization of steam.

Solution

Heat given out by the heater = P t = 600 × 6 × 60

Heat absorbed by steam = 0.10 × L v

Heat gained = heat lost, therefore, 600 × 6 × 60 = 0.10 × L v = 2.16 × 106 J / Kg

Evaporation

Factors affecting the rate of evaporation

a) Temperature

b) Surface area

c) Draught (hot and dry surrounding)

d) Humidity

Comparison between boiling and evaporation Evaporation Boiling

1. Takes place at all temperature - takes place at a specific temperature

2. Takes place on the surface (no bubbles formed)- takes place throughout the liquid ( bubbles formed)

3. Decrease in atmospheric pressure increases the rate –decreases as atmospheric pressure lowers

Applications of cooling by evaporation

a) Sweating

b) Cooling of water in a porous pot

c) The refrigerator

Chapter Ten

The Gas Laws

Pressure law This law states that “the pressure of a fixed mass of a gas is directly proportional to the absolute temperature if the volume is kept constant”. The comparison between Kelvin scale and degrees Celsius is given by; θ0 = (273 + θ) K, and T (K) = (T – 273) 0C.

Examples

1. A gas in a fixed volume container has a pressure of 1.6 × 105 Pa at a temperature of 27 0C.

What will be the pressure of the gas if the container is heated to a temperature of 2770C?

Solution

Since law applies for Kelvin scale, convert the temperature to kelvin

T1 = 270C = (273 + 27) K = 300 K

T2 = 2270C = (273 + 277) = 550 K

P₁ / T₁ = P₂ / T₂, therefore P₂ = (1.6 × 105) × 550 / 300 = 2.93 × 105 Pa.

2. At 200C, the pressure of a gas is 50 cm of mercury. At what temperature would the pressure of the gas fall to 10 cm of mercury?

Solution

P / T = constant, P₁ / T₁ = P₂ / T₂, therefore T₂= (293 × 10) / 50 = 58.6 K or (– 214.4 0C)

Charles law

Charles law states that “the volume of a fixed mass of a gas is directly proportional to its absolute temperature (Kelvin) provided the pressure is kept constant”. Mathematically expressed as follows,

V1 / T1 = V2 / T2

Examples

1. A gas has a volume of 20 cm³ at 270C and normal atmospheric pressure.

Calculate the new volume of the gas if it is heated to 540C at the same pressure.

Solution

Using, V₁ / T₁ = V₂ / T₂, then V₂ =(20 × 327) / 300 = 21.8 cm³.

2. 0.02m³ of a gas is at 27 0C is heated at a constant pressure until the volume is 0.03 m³. Calculate the final temperature of the gas in 0C.

Solution

Since V₁ / T₁ = V₂ / T₂, T₂ = (300 × 0.03) / 0.02 = 450 K 0r 1770C

Boyle’s law

Boyle’s law states that “the pressure of a fixed mass of a gas is inversely proportional to its volume provided the temperature of the gas is kept constant”.

Mathematically expressed as,

P₁ V₁ = P₂ V₂

Examples

1. A gas in a cylinder occupies a volume of 465 ml when at a pressure equivalent to 725 mm of mercury. If the temperature is held constant, what will be the volume of the gas when the pressure on it is raised to 825 mm of mercury?

Solution

Using, P₂ V₁ = P₂ V₂, then V₂ = (725 × 465) / 825 = 409 ml.

2. The volume of air 26 cm long is trapped by a mercury thread 5 cm long as shown below. When the tube is inverted, the air column becomes 30 cm long. What is the value of atmospheric pressure?

Solution

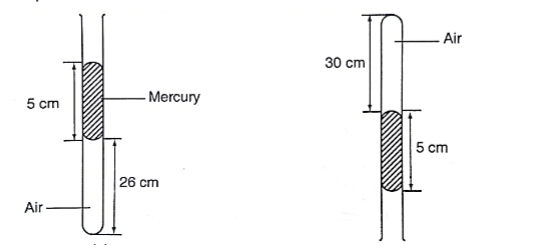
Before inversion, gas pressure = atm. Pressure + h p g

After inversion, gas pressure = atm. Pressure - h p g

From Boyle’s law, P1 V1 = P2 V2, then let the atm. Pressure be ‘x’,

So (x + 5) 0.26 = (x – 5) 0.30

0.26x + 1.30 = 0.3x - 1.5, x = 2.8/ 0.04 = 70 cm.

A general gas law

Any two of the three gas laws can be used derive a general gas law as follows,

P₁ V₁ / T₁ = P₂ V₂ / T₂ or

P V / T = constant – equation of state for an ideal gas.

Examples

1. A fixed mass of gas occupies 1.0 × 10^-3 m³ at a pressure of 75 cmHg. What volume does the gas occupy at 17.0 0C if its pressure is 72 cm of mercury?

Solution

P V / T = constant so V₁= (76 × 1.0 × 10-3 × 290) / 273 ×72 = 1.12 × 10^-3 m³

2. A mass of 1,200 cm³ of oxygen at 270C and a pressure 1.2 atmosphere is compressed until its volume is 600 cm³ and its pressure is 3.0 atmosphere. What is the Celsius temperature of the gas after compression?

Solution

Since P₁ V₁ / T₁ = P₂ V₂ / T₂, then T₂ = (3 × 600 × 300) / 1.2 × 1,200 = 375 K or 102 0C.

KCSE Revision Notes Form 1 - Form 4 All Subjects

Agriculture Form 1 Notes

Agriculture Form 2 Notes

Agriculture Form 3 Notes

Agriculture Form 4 Notes

Agriculture Notes Primary Tillage

Betrayal in the City by Francis Imbuga

Biology Diagrams and Images

Biology Questions and Answers Form One

Biology Questions and Answers Form Two

Biology Questions and Answers Form Three

Biology Questions and Answers Form Four

Business Studies Notes KCSE Form 1 - 4 | Business Notes for Secondary Schools in Kenya

Chemistry Notes - Acid, Bases and Indicators

Chemistry Notes - Acid, Bases and Salts

Chemistry Notes Form 1

Chemistry Notes Form 2

Chemistry Notes Form 3

Computer Studies Notes Form 1

Computer Studies Notes Form 2

Computer Studies Notes Form 3

Computer Studies Notes Form 4

CRE Notes - Christian Religious Education Revision

CRE Notes - Christian Religious Education Questions and Answers

English Grammar Notes

English Moral Stories and Composition Ideas

History and Government Notes Form 1 to Form 4

History and Government Questions and Answers

Home Science Form 1 Notes

Home Science Form 2 Notes

Home Science Form 3 Notes

Home Science Form 4 Notes

How to Revise Efficiently for KCSE Exams

Geography Notes Form 1

Geography Notes Form 2

Geography Notes Form 3

Geography Notes Form 4

Physics Notes Form 1 to 4

The River and the Source

More Biology Notes - Biology Study Guide

KCSE Revision Notes Form 1 to Form 4 - All Subjects - Free Download - KCSE - Download Free KCSE Form 1 2 3 4 Notes - KCSE Revision

KCPE Results » List of National Schools in Kenya (Classified According to Clusters) » National Secondary Schools in Kenya » List of All Secondary Schools in Kenya Per County » Form 1 Intake - Selection Criteria, Selection List » KCSE Results » Secondary Schools in Kenya » KNEC - Kenya National Examinations Council KCPE Results Performance » KNEC - Kenya National Examinations Council » KCSE Results

Secondary School Scholarships in Kenya » Kenya Postgraduate Scholarships » Undergraduate Scholarships for Kenyan Students » Kenya Scholarships for Kenyan Students Studying in Kenya » Kenya Undergraduate Scholarships » The Kenya Youth Education Scholarship Fund - Scholarships Kenya - Scholarships KCSE Results » KCSE Results Top 100 Schools - Kenya Certificate of Secondary Education – KCSE » KCSE Top 100 Candidates » Kenya Certificate of Secondary Education – KCSE » KNEC - Kenya National Examinations Council » Secondary Schools in Kenya » KNEC - Kenya National Examinations Council » Free KNEC KCSE Past Papers

Kenya Scholarships for Undergraduate Students » Kenya Scholarships for Postgraduate Students » Undergraduate Scholarships for Kenyan Students » Kenya Undergraduate Scholarships » Full Undergraduate Scholarships for Kenyans » Kenya Postgraduate Scholarships » Scholarships & Grants » Undergraduate Scholarships » Universities in Kenya » Kenya Universities and Colleges Central Placement Service (KUCCPS) » Colleges in Kenya » KASNEB Registration & Results » Secondary Schools Scholarships in Kenya » Undergraduate & Graduate Scholarships for Kenyans

Powerful Motivational Quotes for Students » Success Quotes for Students » KCSE Motivational Quotes for KCSE Candidates » KCSE Success Quotes for KCSE Candidates

a a a physics notes! chapter 1 introduction to physics college physics notes download klb physics book 4 download physics notes form 3 electronics form four notes form 1 past papers form 1 past papers with answers form 1 physics notes form 1 physics questions and answers form 1 physics revision notes form 1 physics syllabus form 1 physics test paper pdf form 2 physics exam paper form 2 physics exam paper 2016 form 2 physics exam paper free download form 2 physics exam paper with answer form 2 physics final year exam paper 2 form 2 physics past papers form 2 physics revision notes form 2 physics short notes form 2 physics syllabus form 3 past papers form 3 physics exam paper form 3 physics notes form 3 physics past papers form 3 physics questions form 3 physics questions and answers pdf form 3 physics revision notes form 3 physics syllabus form 4 exam papers form 4 physics notes form 4 physics revision notes form 4 physics syllabus form 4 physics topics form 5 physics topics form five physics notes form four physics notes form four physics questions and answers form four physics questions and answers pdf form four physics topics form four revision papers form one exams form one past papers form one physics examination form one physics past papers pdf form one physics questions and answers form one physics questions and answers pdf form one physics topics form one term one physics exam form three physics notes form three physics notes pdf form three physics questions and answers form three physics questions and answers pdf form three physics topics form two notes form two physics notes form two physics notes pdf form two physics questions and answers form two physics questions and answers pdf form two physics syllabus form two physics topics high school physics notes high school physics study guide introduction of physics form one introduction to physics notes k.l.b physics notes kcse physics notes kcse physics syllabus kenya secondary school physics syllabus pdf klb physics book 1 pdf klb physics book 2 pdf klb physics book 3 pdf klb physics book 3 pdf download klb physics book 4 notes klb physics book 4 pdf klb physics book 4 pdf download klb physics book 4 topics klb physics form 1 klb physics form 1 pdf klb physics form 2 klb physics form 2 notes klb physics form 2 pdf klb physics form 2 pdf download klb physics form 3 klb physics form 3 pdf klb physics form 3 pdf download klb physics form 4 klb physics form 4 pdf klb physics form four notes klb physics form one notes klb physics form three notes klb physics form two notes klb physics notes klb physics notes form 4 klb physics pdf maktaba tetea notes necta form four past papers necta past papers form 4 2016 necta past papers form six necta past papers form two necta physics past papers necta physics practicals necta questions and answers necta review questions notes za physics form one notes za physics form three past papers 2014 physic form 4 chapter 1 mind map physic notes physics book 4 pdf physics exam form three physics form 1 exams physics form 1 mid year exam physics form 1 past papers physics form 1 pressure physics form 1 questions and answers physics form 1 questions and answers pdf physics form 2 exam paper 2014 physics form 2 exams physics form 2 notes physics form 2 past papers physics form 2 pdf physics form 2 questions and answers physics form 2 questions and answers pdf physics form 3 exams physics form 3 notes pdf physics form 3 past papers physics form 3 questions and answers physics form 3 syllabus physics form 4 chapter 1 conversion of units physics form 4 chapter 1 exercise physics form 4 chapter 1 exercise and answers physics form 4 chapter 1 exercise pdf physics form 4 chapter 1 mind map physics form 4 chapter 2 physics form 4 chapter 2 exercise and answers physics form 4 chapter 2 exercise pdf physics form 4 chapter 2 experiment physics form 4 chapter 2 formula physics form 4 chapter 2 mind map physics form 4 chapter 2 momentum physics form 4 chapter 2 notes pdf physics form 4 chapter 2 objective questions and answers physics form 4 chapter 2 paper 2 physics form 4 chapter 2 slideshare physics form 4 chapter 3 physics form 4 chapter 3 questions and answers physics form 4 chapter 4 notes pdf physics form 4 chapter 5 light questions and answers physics form 4 chapter 5 notes pdf physics form 4 exam paper 1 physics form 4 exams physics form 4 exercise physics form 4 exercise pdf physics form 4 module with answer physics form 4 notes chapter 1 physics form 4 notes free download physics form 4 notes pdf physics form 4 paper 2 questions and answers physics form 4 past papers physics form 4 questions and answers physics form 4 revision notes physics form 5 chapter 1 exercise and answers physics form 5 chapter 1 notes pdf physics form 5 chapter 2 notes pdf physics form 5 chapter 2 slideshare physics form 5 chapter 3 notes pdf physics form 5 notes pdf physics form four book physics form four notes pdf physics form four questions physics form four study notes physics form four topics physics form one physics form one book physics form one notes physics form one notes pdf physics form one study notes physics form three book physics form three notes physics form three study notes physics form two book physics form two notes physics form two notes pdf physics form two questions physics form two study notes physics form two topics physics module form 5 physics notes physics notes for class 11 pdf physics notes for class 12 pdf physics notes form 1 free download physics notes igcse physics notes pdf physics simple notes physics spm notes download physics spm notes pdf physics spm questions physics study guide answers physics study guide pdf physics study guides radioactivity form four secondary physics notes pdf spm notes success physics spm pdf tahossa past papers

1 a a kcse past papers 2014 kcse marking schemes 2016 kcse papers 2016 kcse prediction questions 2018 kcse exam 2018 kcse questions a a kcse past papers advance-africa.com kcse rev quiz agriculture mock papers agriculture paper 2 questions and answers pdf alliance mocks 2017 ap biology essay questions and answers arabic exam 2016 arabic oral exam questions betrayal in the city essay questions and answers pdf betrayal in the city essay questions with answers betrayal in the city, ,,revision questions biology book 3 klb biology essay questions and answers form 4 biology essay questions and answers form 4 pdf biology essays pdf biology exam questions and answers pdf biology form 2 questions and answers pdf biology form 3 notes pdf biology form 3 questions and answers pdf biology form 3 syllabus biology form three reproduction biology form three-questions and answers biology kcse - kcse biology questions and answers - kcse biology essay questions and answers - kcse biology paper 1 2015 - kcse biology notes - kcse 2015 biology paper 2 - kcse biology practical 2015 - kcse biology practicals - kcse biology 2011

biology kcse 2017 biology kcse questions biology paper 1 questions and answers biology paper 2 questions and answers biology paper 3 questions and answers biology questions and answers for high schools biology questions and answers for high schools pdf biology questions and answers form 2 biology questions and answers multiple choice biology questions and answers on cells biology questions and answers online biology questions and answers pdf biology revision notes form 3 business past kcse past papers c.r.e form one notes pdf cambridge igcse computer science cambridge igcse computer science answers cambridge igcse computer science coursebook pdf download cambridge igcse computer science revision guide pdf cambridge igcse computer science study and revision guide pdf cambridge igcse computer science workbook - free download cambridge igcse computer science workbook pdf caucasian chalk circle essay questions chemistry paper 1 questions and answers chemistry paper 2 questions and answers chemistry paper 3 question and answer chemistry past papers form 1 chemistry past papers form 2 cie past papers computer science 0478 computer science igcse past papers xtremepapers computer science paper 2 2017 computer science past papers a level computer science past papers o level computer studies form 1 questions computer studies form 3 past papers computer studies past papers computer studies questions and answers pdf county mocks 2017 cre form 2 notes pdf cre form 3 notes cre form 3 notes pdf cre form 4 notes cre form 4 notes pdf cre form one notes cre kcse 2016 cre notes cre notes form 2 cre notes pdf cre paper 1 with answers cre paper 2 cre paper 2 topics cre preparation notes cre questions form one cre revision notes cre revision questions and answers download kcse past papers with answers dvance kcse past papers edexcel igcse computer science past papers english paper 3 question paper - 2014 kcse english paper 3 question paper - 2015 kcse english paper 3 question paper - 2016 kcse english paper 3 question paper - 2017 kcse english paper 3 question paper - 2018 kcse essay questions and answers on betrayal in the city essay questions based on betrayal in the city find download kcse past papers with answers - kcse past papers pdf download - kcse 2013 marking scheme - kcse mathematics past papers pdf - free kcse past papers and marking schemes - kcse mock papers pdf - kcse past papers 2014 pdf - kcse past papers 2015 - kcse past papers 2010 find kcse biology essay questions and answers - kcse biology practicals - kcse biology paper 1 2015 - biology essay questions and answers form 4 - kcse biology questions and answers - ap biology essay questions and answers - kcse biology notes - kcse biology paper 2 2012 - kcse biology paper 2 2015

form 2 biology questions and answers free kcse mocks 2015 free kcse past papers - kcse past papers - knec kcse online past papers - knec kcse results past papers free kcse past papers 2014 free kcse past papers kenya, free marking schemes, download ... free kcse past papers with answers free kcse questions and answers on chemistry free revision papers general biology test questions and answers general science questions and answers pdf history and government paper one topics history form one questions and answers pdf history paper 1 questions and answers history paper 2 questions and answers home science past papers igcse computer science book igcse computer science book pdf download igcse computer science notes igcse computer science paper 2 notes igcse computer science past papers igcse computer science past papers 2014 igcse computer science past papers 2017 igcse computer science pdf igcse computer science pre release material 2018 igcse computer science resources igcse computer science revision notes pdf igcse computer science workbook pdf igcse computer studies past papers interesting biology questions ire kcse past papers k.c.s.e cre paper 1 2017 k.c.s.e geography 2017 k.c.s.e mathematics paper 1 2017 k.c.s.e mocks 2018 k.c.s.e past papers 2014 kcpe 2018 predictions kcpe prediction questions kcse 2010 marking scheme kcse 2010 past papers kcse 2011 cre paper 1 kcse 2011 marking scheme kcse 2012 history paper 2 marking scheme kcse 2012 marking schemes kcse 2013 cre paper 1 kcse 2013 marking scheme kcse 2013 marking scheme pdf kcse 2014 kcse 2015 biology paper 2 kcse 2015 biology paper 3 kcse 2015 marking scheme kcse 2015 past papers kcse 2016 agriculture paper 2 kcse 2016 biology paper 1 kcse 2016 biology paper 2 kcse 2016 computer paper 1 kcse 2017 marking scheme kcse 2017 maths paper 1 kcse 2017 papers kcse 2017 papers and marking scheme kcse 2017 past papers kcse 2017 prediction pdf kcse 2018 cre prediction kcse 2018 leakage kcse 2018 marking scheme kcse 2018 papers kcse 2018 predictions kcse 2019 marking scheme kcse agriculture past papers kcse answers kcse arabic paper 1 kcse arabic paper 2 kcse arabic paper 3 kcse arabic paper 3 2016 kcse arabic past papers kcse biology 2011 kcse biology essay questions and answers kcse biology essay questions and answers - kcse revision questions and answers - kcse chemistry questions and answers - kcse revision papers with answers - kcse past papers with answers - download kcse past papers with answers - kcse questions on the river and the source - kcse revision notes

kcse biology essay questions and answers - kcse revision questions and answers - kcse chemistry questions and answers - kcse revision papers with answers - kcse past papers with answers - download kcse past papers with answers - kcse questions on the river and the source - kcse revision notes

kcse biology essay questions and answers pdf kcse biology essays kcse biology essays pdf kcse biology notes kcse biology paper 1 kcse biology paper 1 2017 kcse biology paper 1 2017 pdf kcse biology paper 2 2012 kcse biology paper 2 2015 kcse biology paper 2 2017 kcse biology paper 3 2016 kcse biology paper 3 past papers kcse biology past papers kcse biology past papers and answers kcse biology practical 2016 kcse biology practical past papers kcse biology practicals kcse biology questions and answers kcse biology questions and answers - kcse past papers biology - kcse biology essay questions and answers - kcse chemistry past papers - download kcse past papers with answers - k.c.s.e papers 2015 - k.c.s.e papers 2016 - kcse biology paper 1 2015 - kcse past papers 2015 - kcse past papers 2011 - kcse past papers 2016 - kcse past papers 2017 - 2017 kcse prediction questions - 2018 kcse prediction questions

kcse business paper 1 2016 kcse business past papers kcse business studies past papers kcse chemistry paper 1 2016 kcse chemistry paper 1 2017 kcse chemistry paper 3 2012 kcse chemistry past papers kcse chemistry past papers and answers kcse chemistry practical kcse computer studies paper 1 kcse computer studies paper 2 kcse computer studies paper 2 pdf kcse cre 2016 kcse cre paper 1 2013 kcse cre paper 1 2015 kcse cre paper 1 2016 kcse cre paper 1 2017 kcse cre paper 2 kcse cre paper 2 2016 kcse cre past papers kcse cre past papers and answers kcse english paper 3 2016 kcse english paper 3 2017 kcse essay questions in betrayal in the city kcse exam papers 2018 kcse exam papers answers kcse french paper 1 kcse french paper 2 kcse french past papers kcse general science syllabus kcse geography paper 2 2016 kcse history paper 1 2012 kcse history paper 2 2016 kcse history paper 2 2017 kcse kiswahili paper 1 2017 kcse marking scheme 2016 kcse marking schemes kcse marking schemes 2017 kcse marking schemes pdf kcse mathematics marking schemes kcse mathematics paper 1 2015 kcse mathematics paper 1 2016 kcse mathematics paper 2 2016 kcse mathematics past papers kcse mathematics past papers pdf kcse mock exams kcse mock papers 2015 kcse mock papers 2017 kcse mock papers 2018 kcse mock papers pdf kcse mock papers pdf 2018 kcse mocks 2017 kcse mocks 2018 kcse music past papers kcse online past papers kcse papers 2015 kcse past papers kcse past papers - kcpe and answers - free mocks online - kcse answers past exams question papers - downloads | kcse papers and marking schemes | exams - kcse mathematics paper 1 questions and answers - kcse cre paper 1 questions and answers - knec past papers free downloads - kcse online registration - kcpe - kcse past papers - knec - knec portal - knec past papers for colleges - kasneb - past papers - kasneb past papers for colleges - cpa past papers - https://www.knec.ac.ke/ - www.knec-portal.ac.ke/ - knec portal: kcse results, online registration, kcse result slip. knec portal confirmation - knec portal kcse results - knec examiners portal - knec website kcse past papers - kcpe and answers - free mocks online - kcse answers past exams question papers - downloads | kcse papers and marking schemes | exams - kcse mathematics paper 1 questions and answers - kcse cre paper 1 questions and answers

kcse past papers 2007 kcse past papers 2009 kcse past papers 2010 kcse past papers 2011 kcse past papers 2011 pdf kcse past papers 2012 kcse past papers 2013 kcse past papers 2013 -knec kcse past papers 2014 kcse past papers 2014 pdf kcse past papers 2015 kcse past papers 2015 marking schemes kcse past papers 2015 pdf kcse past papers 2016 kcse past papers 2016 pdf kcse past papers 2017 kcse past papers 2017 pdf kcse past papers agriculture and answers kcse past papers arabic and answers kcse past papers art and design and answers kcse past papers biology kcse past papers building and construction and answers kcse past papers business studies and answers kcse past papers chemistry kcse past papers chemistry and answers kcse past papers chemistry pdf kcse past papers computer studies and answers kcse past papers cre and answers kcse past papers electricity and answers kcse past papers english and answers kcse past papers french and answers kcse past papers general science and answers kcse past papers geography and answers kcse past papers german and answers kcse past papers history and government and answers kcse past papers home science and answers kcse past papers hre and answers kcse past papers ire and answers kcse past papers kenya sign language and answers kcse past papers kiswahili and answers kcse past papers marking scheme kcse past papers maths kcse past papers metal work and answers kcse past papers music and answers kcse past papers pdf download kcse past papers physics and answers kcse past papers physics with answers kcse past papers power mechanics and answers kcse past papers with answers kcse past papers woodwork and answers kcse physics past papers kcse prediction 2017 kcse prediction 2018 kcse prediction 2018 pdf kcse prediction papers 2018 kcse prediction questions 2018 kcse prediction questions and answers kcse questions and answers kcse questions and answers. download free kcse past papers from knec. all marking schemes - questions and answers are sourced from knec. kcse revision kcse revision papers 2014 kcse revision | secondary school | text books | text book centre kcse trial 2017 kcse trial exams 2017 kenyaplex kcse past papers kenyaplex past papers for secondary kiswahili paper 3 questions and answers klb biology form 3 pdf klb cre form 1 klb cre form 3 knec ict past papers knec past papers for colleges knec past papers free download knec past papers pdf knec revision papers knec technical exams past papers kusoma.com past papers maths kcse 2017 mock past papers 2017 mock past papers with answers mokasa mock 2017 page navigation papacambridge computer science igcse past kcse papers past papers in kenya pre mocks 2018 pte knec past papers revision sample essays on betrayal in the city school biology notes school geography notes school physics notes school river and the source themes used in betrayal in the city xtremepapers igcse computer science z notes computer science igcse

Physics Notes Form 3

"Pdf" Revision Questions Physics Form 1 "Pdf" Revision Questions Physics Form 2 "Pdf" Revision Questions Physics Form 3 "Pdf" Revision Questions Physics Form 4 "Pdf" Revision Questions Physics Form Four "Pdf" Revision Questions Physics Form One "Pdf" Revision Questions Physics Form Three "Pdf" Revision Questions Physics Form Two 1 a a KCSE Past Papers 10th Grade Physics Questions and Answers 10th Grade Physics Test 11th Ncert Physics 12th Class Physics Book Free Download 2014 KCSE Marking Schemes 2014 Pdf KCSE Past Papers 2015 2015 Physics Essay Questions and Answers Form 4 2016 KCSE Papers 2016 KCSE Prediction Questions 2017 Physics Hsc Answers 2017 KCSE Prediction Questions 2018 Physics KCSE Leakage 2018 Physics KCSE Questions 2018 KCSE Busineness Studies 2018 KCSE Exam 2018 KCSE Leakage 2018 KCSE Prediction Questions 2018 KCSE Questions 2019 Physics KCSE Leakage 2019 Physics KCSE Questions 2019 KCSE Leakage 2019 KCSE Questions 9th Grade Physics Study Guide A a a Physics Notes a a a Physics Notes! a a a PhysicsNotes! A a KCSE Past Papers A Biblical View of Social Justice A Level Physics Biological Molecules Questions A Level Physics Exam Questions by Topic A Level Physics Notes Edexcel A Level Physics Notes Xtremepapers A Level Physics Past Papers A Level Physics Questions and Answers a Level Physics Questions and Answers A Level Physics Questions and Answers (Pdf) A Level Physics Questions and Answers Pdf A Level Physics Questions by Topic Kidney Questions With Markschemes A Level Physics Revision A Level Physics Revision Edexcel A Level Physics Revision Guide A Level Physics Revision Notes A Level Physics Revision Notes Pdf A Level Physics Textbook Pdf A Level Physics Year 1 / as Aqa Exam Questions by Topic A Level Edexcel Notes a* Physics aa Physics Form 3 Questions and Answers Advance KCSE Past Papers Advance-africa.com KCSE Rev Quiz Advantages and Disadvantages. All Physics Essays All Physics Notes for Senior Two All KCSE Past Papers Physics With Making Schemes All Marking Schemes Questions and Answers All Past K.c.s.e Questions With Answers Alliance Mocks 2017 Ap Bio Quizzes Ap Physics 1 Textbook Pdf Ap Physics Essay Questions and Answers Are Sourced From KNEC. As Level Physics Notes Atika Physics Notes Atika School Physics Notes B/s Book 2 Notes Basic Physics Books Pdf basic Physics Interview Questions and Answers Pdf Basic Physics Interview Questions and Answers Pdf Basic Physics Pdf Basic Physics Questions and Answers Basic Physics Questions and Answers Pdf Bbc Bitesize Physics Ks3 Bihar Board Physics Objective Answer 2017 Bihar Board Physics Objective Answer 2018 Bio Answers Bio Quesions Physics 0478 Physics 101 Physics 12th Physics 12th Class Notes Pdf Physics 2019 Syllabus Physics All KCSE Short Notes Physics Answers Physics Answers Online Free Physics Answers Quizlet Physics Bk 2 Notes Physics Book 1 Physics Book 1 Notes Physics Book 2 Physics Book 2 Notes Physics Book 3 Physics Book 3 KLB Physics Book 3 Notes Physics Book 4 Physics Book 4 Notes Physics Book 4 Pdf Physics Book for Class 11 Physics Book Four Physics Book Four Notes Physics Book One Physics Book One Notes Physics Book Pdf Free Download Physics Book Three Physics Book Three Notes Physics Book Three Pdf Physics Book Two Physics Book Two Notes Physics Books Form Three Physics Bowl Physics Study Guide Physics Bowl Questions Physics Physics Bowl Questions Earth Physics Physics Bowl Questions Math Physics Bowl Questions Middle School Physics Brekthrough Form Two Notes Physics Class 12 Ncert Solutions Physics Class 12 Pdf Physics Communication Syllabus Physics Diagram Software Physics Diagrams for Class 11 Physics Diagrams for Class 12 Physics Diagrams for Class 9 Physics Diagrams for Class-10 Physics Diagrams in Form 1 Physics Diagrams in Form 2 Physics Diagrams in Form 3 Physics Diagrams in Form 4 Physics Diagrams Pdf Physics Diagrams to Label Physics Essay Questions and Answers Physics Essay Questions and Answers 2018 Physics Essay Questions and Answers Form 1 Physics Essay Questions and Answers Form 2 Physics Essay Questions and Answers Form 3 Physics Essay Questions and Answers Form 4 Physics Essay Questions and Answers Form 4 Pdf Physics Essay Questions and Answers Pdf Physics Essay Revision Q Physics Essays and Answers Physics Essays Form One to Form Four Physics Essays Form One to Form Three Physics Essays KCSE Physics Essays Pdf Physics Exam 1 Multiple Choice Physics Exam 2 Advance Physics Exam 2 Test Physics Exam 2016 Physics Exam Form Four Physics Exam Form One Physics Exam Form Three Physics Exam Form Two Physics Exam Practice Test Physics Exam Questions Physics Exam Questions and Answers Physics Exam Questions and Answers Pdf Physics Exam Study Guide Physics Exams Physics Excretion Notes Physics Exercise Form 4 With Answers Physics Final Exam Answer Key Physics Final Exam Answer Key 2016 Physics Final Exam Answer Key 2017 Physics Final Exam Answers 2018 Physics Final Exam Answers 2019 Physics Final Exam Questions and Answers Physics Fom 1 Notes Physics Fom 2 Notes Physics Fom 3 Notes Physics Fom 4 Notes Physics Form 1 Physics Form 1 & 2 and Answers Physics Form 1 and 2 Essays Physics Form 1 and 2 Essays Questions and Answers Physics Form 1 Chapter 1 Physics Form 1 Diagrams Physics Form 1 Exams Physics Form 1 Mid Year Exam Physics Form 1 Notes Physics Form 1 Notes and Questions Physics Form 1 Notes Download Physics Form 1 Notes Free Download Physics Form 1 Notes GCSE Physics Form 1 Notes KCSE-kcse Physics Form 1 Notes Pdf Physics Form 1 Notes Pdf Download Physics Form 1 Past Papers Physics Form 1 Pdf Physics Form 1 Pressure Physics Form 1 Question Papers Physics Form 1 Questions Physics Form 1 Questions and Answers Physics Form 1 Questions and Answers Pdf Physics Form 1 Quiz Physics Form 1 Revision Questions Physics Form 1 Summary Notes Physics Form 1 Syllabus Physics Form 1 Work Physics Form 1-4 Notes Physics Form 2 Physics Form 2 Chapter 1 Physics Form 2 Chapter 2 Physics Form 2 Diagrams Physics Form 2 Exam Paper 2014 Physics Form 2 Exams Physics Form 2 Notes Physics Form 2 Notes and Questions Physics Form 2 Notes GCSE Physics Form 2 Notes KCSE-kcse Physics Form 2 Notes Pdf Physics Form 2 Notes Pdf Download Physics Form 2 Past Papers Physics Form 2 Pdf Physics Form 2 Question Papers Physics Form 2 Questions Physics Form 2 Questions and Answers Physics Form 2 Questions and Answers Pdf Physics Form 2 Quiz Physics Form 2 Revision Notes Physics Form 2 Salts Physics Form 2 Structure and Bonding Physics Form 2 Summary Notes Physics Form 2 Syllabus Physics Form 2 Work Physics Form 3 Physics Form 3 and 4 Essays Physics Form 3 and 4 Essays Questions and Answers Physics Form 3 Chapter 3 Physics Form 3 Classification Physics Form 3 Diagrams Physics Form 3 Ecology Physics Form 3 Exams Physics Form 3 Notes Physics Form 3 Notes and Questions Physics Form 3 Notes GCSE Physics Form 3 Notes KCSE-kcse Physics Form 3 Notes Pdf Physics Form 3 Notes Pdf Download Physics Form 3 Notes Topic 1 Physics Form 3 Past Papers Physics Form 3 Pdf Physics Form 3 Question Papers Physics Form 3 Questions Physics Form 3 Questions and Answers Physics Form 3 Questions and Answers Pdf Physics Form 3 Questions and Answers Term 3 Physics Form 3 Questions and Answers+pdf Physics Form 3 Quiz Physics Form 3 Revision Notes Physics Form 3 Revision Questions Physics Form 3 Summary Notes Physics Form 3 Syllabus Physics Form 3 Syllabus Pdf Physics Form 3 Topics Physics Form 3 Work Physics Form 4 Physics Form 4 All Chapter Physics Form 4 Chapter 1 Conversion of Units Physics Form 4 Chapter 1 Exercise Physics Form 4 Chapter 1 Exercise and Answers Physics Form 4 Chapter 1 Exercise Pdf Physics Form 4 Chapter 1 Mind Map Physics Form 4 Chapter 2 Physics Form 4 Chapter 2 Exercise and Answers Physics Form 4 Chapter 2 Exercise Pdf Physics Form 4 Chapter 2 Experiment Physics Form 4 Chapter 2 Formula Physics Form 4 Chapter 2 Mind Map Physics Form 4 Chapter 2 Momentum Physics Form 4 Chapter 2 Notes Pdf Physics Form 4 Chapter 2 Objective Questions and Answers Physics Form 4 Chapter 2 Paper 2 Physics Form 4 Chapter 2 Slideshare Physics Form 4 Chapter 3 Physics Form 4 Chapter 3 Questions and Answers Physics Form 4 Chapter 4 Physics Form 4 Chapter 4 Notes Pdf Physics Form 4 Chapter 5 Light Questions and Answers Physics Form 4 Chapter 5 Notes Pdf Physics Form 4 Diagrams Physics Form 4 Exam Paper 1 Physics Form 4 Exams Physics Form 4 Exercise Physics Form 4 Exercise Pdf Physics Form 4 Module With Answer Physics Form 4 Note Physics Form 4 Notes Physics Form 4 Notes (Pdf) Physics Form 4 Notes All Chapter Pdf Physics Form 4 Notes and Questions Physics Form 4 Notes Chapter 1 Physics Form 4 Notes Chapter 2 Physics Form 4 Notes Chapter 3 Physics Form 4 Notes Download Physics Form 4 Notes Free Download Physics Form 4 Notes GCSE Physics Form 4 Notes KCSE-kcse Physics Form 4 Notes Pdf Physics Form 4 Notes Pdf Download Physics Form 4 Paper 2 Questions and Answers Physics Form 4 Past Papers Physics Form 4 Question Papers Physics Form 4 Questions Physics Form 4 Questions and Answers Physics Form 4 Questions and Answers Pdf Physics Form 4 Quiz Physics Form 4 Revision Notes Physics Form 4 Schemes of Work Physics Form 4 Summary Notes Physics Form 4 Syllabus Physics Form 4 Textbook Pdf Physics Form 4 Work Physics Form 5 Chapter 1 Exercise and Answers Physics Form 5 Chapter 1 Notes Pdf Physics Form 5 Chapter 2 Notes Pdf Physics Form 5 Chapter 2 Slideshare Physics Form 5 Chapter 3 Notes Pdf Physics Form 5 Notes Pdf Physics Form Four Book Physics Form Four Notes Physics Form Four Notes and Questions Physics Form Four Notes GCSE Physics Form Four Notes Pdf Physics Form Four Past Papers Physics Form Four Questions Physics Form Four Questions and Answers Physics Form Four Questions and Answers Pdf Physics Form Four Quiz Physics Form Four Study Notes Physics Form Four Syllabus Physics Form Four Topic 2 Physics Form Four Topic 4 Physics Form Four Topics Physics Form Four Work Physics Form One Physics Form One Book Physics Form One Book Pdf Physics Form One Download Topic 1 Upto 3 Physics Form One Exam Physics Form One Notes Physics Form One Notes and Questions Physics Form One Notes GCSE Physics Form One Notes Pdf Physics Form One Pdf Physics Form One Questions Physics Form One Questions and Answers Physics Form One Questions and Answers Pdf Physics Form One Questions and Their Answers Physics Form One Quiz Physics Form One Revision Question Physics Form One Schemes of Work Physics Form One Study Notes Physics Form One Syllabus Physics Form One Term Three Test Physics Form One to Three Notes Physics Form One Work Physics Form Three Physics Form Three Book Physics Form Three Notes Physics Form Three Notes and Questions Physics Form Three Notes GCSE Physics Form Three Questions and Answers Physics Form Three Questions and Answers Pdf Physics Form Three Quiz Physics Form Three Reproduction Physics Form Three Reproduction. Physics Form Three Study Notes Physics Form Three Work Physics Form Three-questions and Answers Physics Form Two Physics Form Two Book Physics Form Two Diagrams Physics Form Two Notes Physics Form Two Notes and Questions Physics Form Two Notes GCSE Physics Form Two Notes Pdf Physics Form Two Notes-pdf Physics Form Two Pdf Physics Form Two Questions Physics Form Two Questions and Answers Physics Form Two Questions and Answers Pdf Physics Form Two Quiz Physics Form Two Study Notes Physics Form Two Topics Physics Form Two Work Physics Form Two,schemes of Work Physics Form2 Physics Form2 Textbook Physics Game Form Four Question End Answers Physics Grade 10 Exam Papers Physics Hsc Pdf Physics Human Reproduction Video Physics IGCSE Past Papers Xtremepapers Physics K.c.s.e 2017 Physics KCSE Physics KCSE 2016 Physics KCSE 2017 Physics KCSE 2017 Paper 1 Physics KCSE Past Papers Physics KCSE Questions Physics KCSE Questions and Answer Physics KCSE Quizzes & Answers Physics KCSE Revision Physics KCSE Revision Notes Physics KCSE Setting Questions Form One and Two Physics Ksce 2015 Physics Last Year K.c.s.e Questions Physics Lesson Plan Form Two Physics Made Familiar Physics Mcq for Class 11 Physics Mcq for Class 12 Physics Mcq for Competitive Exams Physics Mcq for Competitive Exams Pdf Physics Mcq for Neet Pdf Physics Mcq for Ssc Physics Mcq Questions With Answers Physics Mcq With Answers Pdf Physics Mcqs for Class 12 Pdf Physics Mcqs With Answers Pdf Physics Mid Familia Form One Physics Mock Papers Physics Module Form 5 Physics Multiple Choice Questions and Answers Cxc Physics Multiple Choice Questions and Answers Pdf Physics Multiple Choice Questions With Answers Pdf Physics Note Physics Note Form Two All Chapters Physics Notes Physics Notes and Guestion and Answear Physics Notes and Syllabus Physics Notes Class 10 Physics Notes for Class 11 Pdf Physics Notes for Class 12 Pdf Physics Notes for High School Students Physics Notes for IGCSE 2014 Physics Notes Form 1 Physics Notes Form 1 4 Physics Notes Form 1 Free Download Physics Notes Form 1 KLB Physics Notes Form 1 Pdf Physics Notes Form 1-4 Physics Notes Form 1-4(1) Physics Physics Notes Form 14 Physics Notes Form 2 Physics Notes Form 2 KLB Physics Notes Form 2 Pdf Physics Notes Form 2; Physics Notes Physics Notes Form 3 Physics Notes Form 3 KLB Physics Notes Form 3 Pdf Physics Notes Form 4 Physics Notes Form 4 Chapter 2 Physics Notes Form 4 KLB Physics Notes Form 4 Pdf Physics Notes Form 4-pdf Physics Notes Form Four Physics Notes Form Four KLB Physics Notes Form Four Pdf Physics Notes Form One Physics Notes Form One KLB Physics Notes Form One Pdf Physics Notes Form One to Form Four Physics Notes Form Three Physics Notes Form Three KLB Physics Notes Form Three Pdf Physics Notes Form Two Physics Notes Form Two KLB Physics Notes Form Two Pdf Physics Notes Form2 Physics Notes IGCSE Physics Notes Kenya Physics Notes on Agroforestry Physics Notes Pdf Physics Notes: Physics Objective Answer Physics Objective Answer 2018 Physics Objective Questions for Competitive Exams Physics Objective Questions for Competitive Exams Pdf Physics Oral Exam Questions Physics Paper 1 Physics Paper 1 2018 Marking Rules Physics Paper 1 Notes Physics Paper 1 Questions Physics Paper 1 Questions and Answers Physics Paper 1 Topics Physics Paper 1 With Answers Physics Paper 2 Physics Paper 2 2017 Physics Paper 2 2018 Marking Rules Physics Paper 2 Questions and Answers Physics Paper 2 Questions and Answers Pdf Physics Paper 2 Revision Physics Paper 2 Topics Physics Paper 2018 Physics Paper 3 2018 Marking Rules Physics Paper 3 Question and Answer Physics Paper 3 Question Paper 2014 KCSE Physics Paper 3 Question Paper 2015 KCSE Physics Paper 3 Question Paper 2016 KCSE Physics Paper 3 Question Paper 2017 KCSE Physics Paper 3 Question Paper 2018 KCSE Physics Paper 3 Questions and Answers Physics Paper One Questions and Answers Physics Paper One Topics Physics Paper Two Qestions With Answers Physics Paper1 Physics Paper2 Physics Paper3 Physics Paper4 Physics Past Papers Physics Past Papers 2017 Physics Past Papers a Level Physics Past Papers Form 1 Physics Past Papers Form 2 Physics Past Papers Form 3 Physics Past Papers O Level Physics Pdf Download Physics Pp1 KCSE 2016 Physics Practical Book Class 12 Pdf Physics Practical Exam Physics Practicals Form One Physics Practicals Questions and Answers Physics Practice Test 9th Grade Physics Practice Test Answers Physics Practice Test Questions and Answers Physics Practice Test Quizlet Physics Predicted Questions This Year KCSE Physics Preparation Notes Physics Pretest High School Pdf Physics Question and Answer With Explanation Physics Question and Answers 2019 Physics Question and Answers 2020 Physics Question and Answers 2021 Physics Question and Answers 2022 Physics Question and Answers Note Physics Questions Physics Questions and Answers Physics Questions and Answers for High School Physics Questions and Answers for High Schools Physics Questions and Answers for High Schools Pdf Physics Questions and Answers for Secondary Schools Physics Questions and Answers Form 1 Physics Questions and Answers Form 2 Physics Questions and Answers Form 3 Physics Questions and Answers Form 4 Physics Questions and Answers Multiple Choice Physics Questions and Answers Notes Physics Questions and Answers O Physics Questions and Answers Online Physics Questions and Answers Pdf Physics Questions and Answers Pdf for Class 12 Physics Questions and Answers Pdf for Competitive Exams Physics Questions and Answers-form 2 Physics Questions for High School Physics Questions for High School Students With Answers Physics Questions for Senior 1 Physics Questions for Senior 2 Physics Questions for Senior 3 Physics Questions for Senior 4 Physics Questions for Senior 5 Physics Questions for Senior 6 Physics Questions for Senior Five Physics Questions for Senior Four Physics Questions for Senior One Physics Questions for Senior Six Physics Questions for Senior Three Physics Questions for Senior Two Physics Questions Form One Physics Questions Multiple Choice Physics Questions Quizlet Physics Questions to Ask Your Teacher Physics Quetion and Answer Form Four Physics Quetion and Answer Form One Physics Quetion and Answer Form Three Physics Quetion and Answer Form Two Physics Quiz for Class 9 Physics Quiz for Class 9 Physics Physics Quiz Questions and Answers for Class 10 Physics Quiz Questions and Answers for Class 10 Pdf Physics Quiz Questions and Answers for Class 12 Physics Quiz Questions and Answers for Class 9 Physics Quiz Questions and Answers for Class 9 Pdf Physics Quiz Questions and Answers for High School Physics Quiz Questions and Answers Multiple Choice Physics Quiz Questions and Answers Pdf Physics Quiz Questions for Class 12 Physics Quiz Questions for College Students Physics Quiz With Answers Physics Quiz With Answers Pdf Physics Quizlet Physics Revision Physics Revision a Level Physics Revision Physics Notes Physics Physics Revision Exam Physics Revision Examination Physics Revision Form One Physics Revision Notes Physics Revision Notes Physics Physics Revision Notes Form 1 Physics Revision Notes Form 2 Physics Revision Notes Form 3 Physics Revision Notes Form 4 Physics Revision Notes IGCSE Physics Revision Paper One Physics Revision Questions Physics Revision Questions and Answers Physics Revision Questions and Answers Form 1 Physics Revision Questions and Answers Form 2 Physics Revision Questions and Answers Form 3 Physics Revision Questions and Answers Form 4 Physics Revision Questions and Answers Form Four Physics Revision Questions and Answers Form One Physics Revision Questions and Answers Form Three Physics Revision Questions and Answers Form Two Physics Revision Questions Form 1 Physics Revision Questions Form 2 Physics Revision Questions Form 3 Physics Revision Questions Form 4 Physics Revision Questions Form Four Physics Revision Questions Form One Physics Revision Questions Form Three Physics Revision Questions Form Two Physics Revision Quiz Physics Revision Test Physics Secondary School Revision Physics Simple Notes Physics Spm Notes Download Physics Spm Notes Pdf Physics Spm Questions Physics Study Form 2 Physics Study Guide Physics Study Guide Answer Key Physics Study Guide Answers Physics Study Guide Physics Questions and Answers Physics Study Guide Ib Physics Study Guide Pdf Physics Study Guides Physics Study Notes Physics Study Notes Materials Form 1 Pdf Physics Study Notes Materials Form 2 3 Pdf Physics Study Notes Materials Form 2 Pdf Physics Study Notes Materials Form 3 Pdf Physics Study Notes Materials Form 4 Pdf Physics Syllabus in Kenya Physics Syllabus Pdf Physics Test 1 Quizlet Physics Test Questions Physics Test Questions and Answers Physics Test Questions and Answers Pdf Physics Topic One Form Four Physics Topics Form One Physics Unit 1 Quiz Physics Vol 3 Physics | Revision Physics Physics,form 4 Physics.form Four.topic Three PhysicsExam Form Three PhysicsModule Form 5 PhysicsNotes PhysicsNotes for Class 11 Pdf PhysicsNotes for Class 12 Pdf PhysicsNotes Form 1 PhysicsNotes Form 1 Free Download PhysicsNotes Form 2 PhysicsNotes Form 3 PhysicsNotes Form 3 Pdf PhysicsNotes IGCSE PhysicsNotes Pdf PhysicsPast Papers PhysicsQuestions and Answers Pdf PhysicsSimple Notes PhysicsSpm Notes Download PhysicsSpm Notes Pdf PhysicsSpm Questions PhysicsStudy Guide Answers PhysicsStudy Guide Pdf PhysicsStudy Guides Blologytextpapers Bridge Physics Business Past KCSE Past Papers Physics Form 3 Notes Pdf Physics Form 4 Notes Pdf C R E Form One KLB C R E Form One Oli Topic C.r.e Form 1 Notes Kenya C.r.e Form 2 Notes Kenya C.r.e Form 3 Notes C.r.e Form 3 Notes Kenya C.r.e Form 3 Pdf C.r.e Form 4 Notes Kenya C.r.e Form One Notes Pdf C.r.e Notes Form 1 C.r.e Revision Notes C.r.e Short Notes Cambridge IGCSE Physics Cambridge IGCSE Physics 3rd Edition Cambridge IGCSE Physics 3rd Edition Plus Cd South Asia Edition Cambridge IGCSE Physics Answers Cambridge IGCSE Physics Coursebook Pdf Download Cambridge IGCSE Physics Practical Workbook Cambridge IGCSE Physics Revision Guide Pdf Cambridge IGCSE Physics Study and Revision Guide 2nd Edition Pdf Cambridge IGCSE Physics Study and Revision Guide Pdf Cambridge IGCSE Physics Workbook Free Download Cambridge IGCSE Physics Workbook Pdf Cambridge IGCSE® Physics Coursebook Caucasian Chalk Circle Essay Questions Chapter 1 Introduction to Physics Chapter 1 Introduction to Physics Studies Cie a Level Physics Notes 2016 Cie a Level Physics Notes Pdf Cie Past Papers Class 10 Physics Chapter 1 Mcqs Class 8 Physics Notes KCSE-kcse College Physics Notes College Physics Practice Test College Physics Quiz College Physics Quiz Chapter 1 College Physics Quizlet College Physics Study Guide College Physics Study Guide Pdf College Physics Test Questions and Answers College Physics Volume 3 Pdf College PhysicsNotes Complete Physics for Cambridge IGCSE Complete Physics for Cambridge IGCSE Revision Guide Pdf County Mocks 2017 Cse Past Papers Physics 2017 Dl Physics Form 3 Pdf Kusoma Download Physics Form 1 Download Physics Form 2 Download Physics Form 2 Notes Download Physics Form 3 Download Physics Form 3 Notes Download Physics Form 4 Download Physics Form Four Download Physics Form One Download Physics Form Three Download Physics Form Two Download Physics Notes Form 3 Download Physics Notes Form One Download PhysicsNotes Form 3 Download Form Three Physics Notes Download Free KCSE Past Papers Physics Download Free KCSE Past Papers From KNEC. Download KCSE Past Papers With Answers Download KCSE Revision Notes Download KLB Physics Book 2 Download KLB Physics Book 3 Download KLB Physics Book 4 Download Notes of Physics Downloads | Physics | Form Four Exams | Exams Downloads | Physics | Form One Exams | Exams Downloads | Physics | Form Three Exams | Exams Downloads | Physics | Form Two Exams | Exams Downloads | KCSE Papers and Marking Schemes | Dvance KCSE Past Papers Easy Physics Questions Edexcel a Level Physics B Edexcel a Level Physics Notes Pdf Edexcel a Level Physics Salters Nuffield Edexcel A2 Physics Notes Edexcel as Physics Revision Guide Pdf Edexcel Physics A2 Revision Notes Pdf Edexcel Physics Unit 2 Revision Notes Edexcel GCSE Physics Revision Guide Pdf Edexcel IGCSE Physics Past Papers Edexcel IGCSE Physics Revision Guide Free Pdf Download Edexcel IGCSE Physics Revision Guide Pdf Edexcel IGCSE Physics Revision Guide Pdf Download Electronics Form Four Notes Energy Questions Physics Bowl Essay Questions and Answers KCSE Physics Notes Essay Questions and Answers on Betrayal in the City Essay Questions Based on Betrayal in the City Evolving World Physics Book 1 Pdf Evolving World Physics Book 4 Notes Evolving World Physics Book Form 1 Evolving World-history Book 3 Exam Notes for Physics 101 Exams KCSE Physics Paper 1 Questions and Answers F3 Physics Test Paper Find Download KCSE Past Papers With Answers Find KCSE Physics Essay Questions and Answers Form 1 Physics Exam Form 1 Physics Notes Form 1 Physics Questions and Answers Form 1 Physics Questions and Answers Pdf Form 1 Physics Revision Notes Form 1 Physics Summurized Revision Pdf Form 1 Physics Syllabus Form 1 Physics Test Paper Pdf Form 1 Physics Topics Form 1 PhysicsNotes Form 1 PhysicsQuestions and Answers Form 1 PhysicsRevision Notes Form 1 PhysicsSyllabus Form 1 PhysicsTest Paper Pdf Form 1 Past Papers Form 1 Past Papers With Answers Form 1 Revision Papers Form 1 Subjects in Kenya Form 2 Physics Exam Form 2 Physics Exam Paper Form 2 Physics Exam Paper 2016 Form 2 Physics Exam Paper Free Download Form 2 Physics Exam Paper With Answer Form 2 Physics Final Year Exam Paper 2 Form 2 Physics Notes Form 2 Physics Notes and Revision Questions Form 2 Physics Notes Pdf Form 2 Physics Past Papers Form 2 Physics Questions Form 2 Physics Questions and Answers Form 2 Physics Questions and Answers > Form 2 Physics Questions and Answers Pdf Form 2 Physics Revision Notes Form 2 Physics Short Notes Form 2 Physics Syllabus Form 2 PhysicsExam Paper Form 2 PhysicsExam Paper Free Download Form 2 PhysicsExam Paper With Answer Form 2 PhysicsFinal Year Exam Paper 2 Form 2 PhysicsPast Papers Form 2 PhysicsRevision Notes Form 2 PhysicsShort Notes Form 2 PhysicsSyllabus Form 2 Revision Papers Form 2 Subjects in Kenya Form 3 Physics Book Form 3 Physics Exam Form 3 Physics Exam Paper Form 3 Physics Notes Form 3 Physics Past Papers Form 3 Physics Questions Form 3 Physics Questions and Answers Form 3 Physics Questions and Answers Pdf Form 3 Physics Revision Notes Form 3 Physics Syllabus Form 3 PhysicsExam Paper Form 3 PhysicsNotes Form 3 PhysicsPast Papers Form 3 PhysicsQuestions Form 3 PhysicsQuestions and Answers Pdf Form 3 PhysicsRevision Notes Form 3 PhysicsSyllabus Form 3 C.r.e Form 3 Notes of Physics Topic on Fish Form 3 Past Papers Form 3 Revision Papers Form 3 Subjects in Kenya Form 4 Physics Exam Form 4 Physics Notes Form 4 Physics Notes Pdf Form 4 Physics Questions and Answers Form 4 Physics Questions and Answers Pdf Form 4 Physics Revision Notes Form 4 Physics Syllabus Form 4 Physics Topics Form 4 PhysicsNotes Form 4 PhysicsRevision Notes Form 4 PhysicsSyllabus Form 4 PhysicsTopics Form 4 Exam Papers Form 4 Revision Papers Form 4 Subjects in Kenya Form 5 Physics Topics Form 5 PhysicsTopics Form Five Physics Notes Form Five PhysicsNotes Form Four Physics Book Form Four Physics Notes Form Four Physics Notes Pdf Form Four Physics Questions and Answers Form Four Physics Questions and Answers Pdf Form Four Physics Revision Questions Form Four Physics Syllabus Form Four Physics Topics Form Four PhysicsNotes Form Four PhysicsQuestions and Answers Form Four PhysicsQuestions and Answers Pdf Form Four PhysicsTopics Form Four Notes Form Four Revision Papers Form Four Subjects in Kenya Form One Physics Book Form One Physics Examination Form One Physics First Topic Form One Physics Lesson Plan Form One Physics Notes Pdf Form One Physics Past Papers Pdf Form One Physics Questions Form One Physics Questions and Answers Form One Physics Questions and Answers Pdf Form One Physics Revision Questions Form One Physics Short Notes Form One Physics Syllabus Form One Physics Topics Form One PhysicsExamination Form One PhysicsPast Papers Pdf Form One PhysicsQuestions and Answers Form One PhysicsQuestions and Answers Pdf Form One PhysicsTopics Form One Exams Form One Notes of Physics Form One Past Papers Form One Subjects in Kenya Form One Term One Physics Exam Form One Term One PhysicsExam Form Three Physics Book Form Three Physics Book Pdf Form Three Physics Notes Form Three Physics Notes Pdf Form Three Physics Questions and Answers Form Three Physics Questions and Answers Pdf Form Three Physics Revision Questions Form Three Physics Syllabus Form Three Physics Topics Form Three PhysicsNotes Form Three PhysicsNotes Pdf Form Three PhysicsQuestions and Answers Form Three PhysicsQuestions and Answers Pdf Form Three PhysicsTopics Form Three Subjects in Kenya Form Two Physics Book Form Two Physics Cat Form Two Physics Examination Form Two Physics Notes Form Two Physics Notes Pdf Form Two Physics Past Papers Form Two Physics Questions and Answers Form Two Physics Questions and Answers Pdf Form Two Physics Revision Questions Form Two Physics Syllabus Form Two Physics Topics Form Two PhysicsNotes Form Two PhysicsNotes Pdf Form Two PhysicsQuestions and Answers Form Two PhysicsQuestions and Answers Pdf Form Two PhysicsSyllabus Form Two PhysicsTopics Form Two Notes Form Two Subjects in Kenya Free a-level Physics Revision App | Pass Your Physics Exams Free Physics Form 1 Notes Free Physics Notes Form 1 Free Physics Notes Pdf Free PhysicsNotes Pdf Free College Physics Practice Test Free Form1,form2,form3 Past Papers Free KCSE Past Papers Free KCSE Mocks 2015 Free KCSE Past Papers 2014 Free KCSE Past Papers KCSE Past Free KCSE Past Papers Kenya, Free KCSE Past Papers With Answers Free KCSE Questions and Answers on Physics Free KCSE Revision Notes Free Marking Schemes Free Mocks Online KCSE Answers Past Exams Question Papers Free Revision Papers From Three Notes Topic One KLB Fun Physics Questions Funny Physics Questions Funny Physics Questions and Answers Funny Physics Questions to Ask Funny Physics Quotes GCSE Physics Exam Questions and Answers GCSE Physics Past Papers GCSE Physics Revision GCSE Physics Revision Notes GCSE Physics Revision Notes Pdf GCSE Physics Revision Notes Pdf 9-1 GCSE Physics Revision Questions and Answers GCSE Physics Textbook Pdf GCSE Physics Topics Pass My Exams: Easy Exam Revision Notes Home Physics Notes Pdf Home Physics Practice Test With Answers Home Physics Quiz Home Physics Quiz Pdf Home Physics Test Questions and Answers Home Physics Test Questions and Answers Pdf Home Knowledge in Physics Human Body Good Physics Questions to Ask GRE Physics Practice Test GRE Physics Subject Test Pdf Handbook of Physics Pdf Free Download Hard Physics Questions Hard Physics Questions and Answers Hard Physics Questions to Ask Your Teacher Hard Physics Quiz Questions Hard Form 3 Physics Question High School Physics Final Exam Doc High School Physics Final Exam Pdf High School Physics Final Exam Questions High School Physics Final Exam Questions and Answers High School Physics Notes High School Physics Practice Test High School Physics Pretest With Answers High School Physics Questions and Answers Pdf High School Physics Study Guide High School Physics Test Questions and Answers Pdf High School PhysicsNotes High School PhysicsStudy Guide How to Answer KCSE Physics Question How to Motivate a Form 4 Student How to Motivate a KCSE Candidate How to Motivate a KCSE Student How to Pass Physics Questions & Answers Form 1&2 | Text Book How to Revise Physics How to Revise Effectively for KCSE How to Study Physics: 5 Study Techniques to Master Physics Hsc Physics 2018 Hsc Physics 2019 Https://www.knec.ac.ke/ Www.knec-portal.ac.ke/ KNEC Portal: Ial Physics Notes Ib Physics Cold War Notes Ib Physics Notes Ib Physics Notes Pdf Ib Physics of the Americas Notes Ib Physics of the Americas Study Guide Ib Physics Paper 2 Study Guide Ib Physics Question Bank by Topic Ib Physics Study Guide Pdf Ict Notes Form 1 IGCSE Physics Alternative to Practical Revision IGCSE Physics Alternative to Practical Revision Notes IGCSE Physics Book IGCSE Physics Book Pdf Download IGCSE Physics Notes IGCSE Physics Notes 2017 Pdf IGCSE Physics Notes Edexcel IGCSE Physics Paper 2 Notes IGCSE Physics Paper 6 Notes IGCSE Physics Past Papers IGCSE Physics Past Papers 2014 IGCSE Physics Past Papers 2017 IGCSE Physics Pdf IGCSE Physics Pre Release Material 2018 IGCSE Physics Resources IGCSE Physics Revision Guide IGCSE Physics Revision Guide Free Download IGCSE Physics Revision Guide Pdf Download IGCSE Physics Revision Notes Pdf IGCSE Physics Revision Worksheets IGCSE Physics Workbook Pdf IGCSE Physics Znotes IGCSE PhysicsPast Papers IGCSE Notes Physics Importance of Agroforestry Inorganic Physics Multiple Choice Questions With Answers Pdf Inorganic Physics Questions and Answers Pdf Interesting Physics Questions Interesting Physics Questions and Answers Interesting Questions to Ask About Physics Intro to Physics Quiz Introduction of Physics Form One Introduction to Physics Introduction to Physics Notes Introduction to Physics Pdf Introduction to PhysicsNotes Is Agroforestry Sustainable? K.c.s.e Answers Physics Paper One 2018 K.c.s.e Physics 2017 K.c.s.e Physics 2018 K.c.s.e Physics Paper 1 2017 K.c.s.e Mocks 2018 K.c.s.e Papers 2015 K.c.s.e Papers 2016 K.c.s.e Past Papers 2014 K.c.s.e.Physics Paper 2 Year 2018 K.c.s.e.results 2018 for Busia County K.l.b Physics Form 3 K.l.b Physics Notes K.l.b PhysicsNotes Kasneb Past Papers for Colleges Physics Past Papers KCSE 2010 Marking Scheme KCSE 2010 Past Papers KCSE 2011 Physics Paper 1 KCSE 2011 Marking Scheme KCSE 2012 Physics Paper 2 Marking Scheme KCSE 2012 Marking Schemes KCSE 2013 Physics Paper 1 KCSE 2013 Marking Scheme KCSE 2013 Marking Scheme Pdf KCSE 2014 KCSE 2015 Physics Paper 2 KCSE 2015 Physics Paper 3 KCSE 2015 Marking Scheme KCSE 2015 Past Papers KCSE 2016 Physics Paper 1 KCSE 2016 Physics Paper 2 KCSE 2017 Physics Paper 1 KCSE 2017 Physics Paper 2 KCSE 2017 Hostory Papers With Answers.com KCSE 2017 Marking Scheme KCSE 2017 Papers KCSE 2017 Papers and Marking Scheme KCSE 2017 Papers Pdf KCSE 2017 Past Papers KCSE 2017 Prediction Pdf KCSE 2018 Physics and Answers KCSE 2018 Physics Prediction KCSE 2018 Leakage KCSE 2018 Marking Scheme KCSE 2018 Papers KCSE 2018 Prediction Pdf KCSE 2018 Predictions KCSE 2018 Questions KCSE 2018 Questions and Answers KCSE 2019 Leakage Physics KCSE 2019 Marking Scheme KCSE 2019 Questions KCSE 2019 Questions and Answers KCSE 2020 Questions KCSE 2020 Questions and Answers KCSE Answers KCSE Answers Past Exams Question Papers Downloads | KCSE Physics 2011 KCSE Physics 2016 KCSE Physics Diagramsbiology Revision Tips KCSE Physics Essay Questions and Answers KCSE Physics Essay Questions and Answers Pdf KCSE Physics Essays KCSE Physics Essays Pdf KCSE Physics Marking Schemes KCSE Physics Notes KCSE Physics Notes Pdf KCSE Physics Notes, Syllabus, Questions, Answers KCSE Physics Paper 1 KCSE Physics Paper 1 2011 KCSE Physics Paper 1 2012 KCSE Physics Paper 1 2013 KCSE Physics Paper 1 2015 KCSE Physics Paper 1 2016 KCSE Physics Paper 1 2017 KCSE Physics Paper 1 2017 Pdf KCSE Physics Paper 1 Questions and Answers KCSE Physics Paper 2 KCSE Physics Paper 2 2012 KCSE Physics Paper 2 2012 KCSE Physics Paper 2 2015 KCSE Physics Paper 2 2013 KCSE Physics Paper 2 2014 KCSE Physics Paper 2 2015 KCSE Physics Paper 2 2016 KCSE Physics Paper 2 2017 KCSE Physics Paper 3 KCSE Physics Paper 3 2012 KCSE Physics Paper 3 2016 KCSE Physics Paper 3 2017 KCSE Physics Paper 3 Past Papers KCSE Physics Past Papers KCSE Physics Past Papers and Answers KCSE Physics Past Papers Pdf KCSE Physics Practical KCSE Physics Practical 2015 KCSE Physics Practical 2016 KCSE Physics Practical Past Papers KCSE Physics Practicals KCSE Physics Practicals KCSE Physics Paper 1 KCSE Physics Question and Answer KCSE Physics Questions and Answers KCSE Physics Questions and Answers Ap Physics KCSE Physics Revision KCSE Physics Revision Notes KCSE Physics Revision Papers KCSE Physics Revision Questions KCSE Physics Revision Questions and Answers KCSE Physics Syllabus KCSE PhysicsNotes KCSE PhysicsPaper 1 KCSE PhysicsPaper 2 KCSE PhysicsPaper 2 Pdf KCSE PhysicsSyllabus KCSE Business Paper 1 2016 KCSE Business Past Papers KCSE Physics Past Papers KCSE Essay Questions in Betrayal in the City KCSE Essays KCSE Exam Papers 2018 KCSE Exam Papers Answers KCSE Form 1 Physics Revision KCSE Form 2 Physics Revision KCSE Form 3 Physics Revision KCSE Form 4 Physics Revision KCSE Form Four Physics Revision KCSE Form One Physics Revision KCSE Form Three Physics Revision KCSE Form Two Physics Revision KCSE KCSE Past Papers KNEC KCSE Leakage KCSE Leakage Physics KCSE Made Familiar Physics KCSE Made Familiar Physics Pdf KCSE Marking Scheme 2016 KCSE Marking Schemes KCSE Marking Schemes 2017 KCSE Marking Schemes Pdf KCSE Mock Exams KCSE Mock Papers 2015 KCSE Mock Papers 2017 KCSE Mock Papers 2018 KCSE Mock Papers Pdf KCSE Mock Papers Pdf 2018 KCSE Mock Papers Pdf KCSE Past Papers KCSE Mocks 2017 KCSE Mocks 2018 KCSE Notes KCSE Online Notes KCSE Online Past Papers KCSE Online Registration KCSE Papers 2015 KCSE Papers and Marking Schemes | Exams KCSE Past Papers KCSE Past Papers 2007 KCSE Past Papers 2009 KCSE Past Papers 2010 KCSE Past Papers 2011 KCSE Past Papers 2011 Pdf KCSE Past Papers 2012 KCSE Past Papers 2013 KCSE Past Papers 2013knec KCSE Past Papers 2014 KCSE Past Papers 2014 Pdf KCSE Past Papers 2015 KCSE Past Papers 2015 Marking Schemes KCSE Past Papers 2015 Pdf KCSE Past Papers 2016 KCSE Past Papers 2016 Pdf KCSE Past Papers 2017 KCSE Past Papers 2017 Pdf KCSE Past Papers 2018 KCSE Past Papers Physics KCSE Past Papers Physics and Answers KCSE Past Papers Physics Pdf KCSE Past Papers Physics With Answers KCSE Past Papers Physicsand Answers KCSE Past Papers Physics and Answers KCSE Past Papers KCSE and Answers KCSE Past Papers KCSE and Answers Free Mocks Online KCSE Past Papers Marking Scheme KCSE Past Papers Pdf Download KCSE Past Papers Pdf Download KCSE 2013 KCSE Past Papers With Answers KCSE Past Papers Woodwork and Answers KCSE Prediction 2017 KCSE Prediction 2018 KCSE Prediction 2018 Pdf KCSE Prediction Papers 2018 KCSE Prediction Questions KCSE Prediction Questions 2018 KCSE Prediction Questions and Answers KCSE Questions KCSE Questions and Answers KCSE Questions and Answers. KCSE Questions on Physics KCSE Results, Online Registration, KCSE Result Slip. KCSE Revision KCSE Revision Notes KCSE Revision Notes Physics KCSE Revision Notes Pdf KCSE Revision Papers KCSE Revision Papers 2014 KCSE Revision Papers With Answers KCSE Revision Question for Physics KCSE Revision Questions KCSE Revision Questions and Answers KCSE Revision | Secondary School | Text Books | Text Book Centre KCSE Syllabus Pdf KCSE Trial 2017 KCSE Trial Exams 2017 Kenya Secondary School Physics Syllabus Kenya Secondary School Physics Syllabus Pdf Kenya Secondary School PhysicsSyllabus Pdf Kenya Secondary School Syllabus Pdf Kenya-kcse-christian Religious Education Syllabus Kenyaplex KCSE Past Papers Kenyaplex Past Papers for Secondary KLB Physics Book 1 Download KLB Physics Book 1 Notes KLB Physics Book 1 Pdf KLB Physics Book 2 KLB Physics Book 2 Notes KLB Physics Book 2 Notes Pdf KLB Physics Book 2 Pdf KLB Physics Book 3 Notes KLB Physics Book 3 Pdf KLB Physics Book 3 Pdf Download KLB Physics Book 4 Notes KLB Physics Book 4 Pdf KLB Physics Book 4 Pdf Download KLB Physics Book 4 Topics KLB Physics Book One KLB Physics Form 1 KLB Physics Form 1 Notes KLB Physics Form 1 Pdf KLB Physics Form 2 KLB Physics Form 2 Book KLB Physics Form 2 Notes KLB Physics Form 2 Pdf KLB Physics Form 2 Pdf Download KLB Physics Form 2 Schemes of Work KLB Physics Form 3 KLB Physics Form 3 Notes KLB Physics Form 3 Notes Pdf KLB Physics Form 3 Pdf KLB Physics Form 3 Pdf Download KLB Physics Form 4 KLB Physics Form 4 Notes KLB Physics Form 4 Pdf KLB Physics Form Four KLB Physics Form Four Notes KLB Physics Form One KLB Physics Form One Notes KLB Physics Form Three KLB Physics Form Three Notes KLB Physics Form Two KLB Physics Form Two Notes KLB Physics Notes KLB Physics Notes Form 4 KLB Physics Pdf KLB PhysicsNotes KLB PhysicsNotes Form 4 KLB PhysicsPdf KNEC Physics Syllabus KNEC Examiners Portal KNEC Website KNEC Ict Past Papers KNEC Past Papers for Colleges KNEC Past Papers Free Download KNEC Past Papers Free Downloads KNEC Past Papers Pdf KNEC Portal Confirmation KNEC Portal KCSE Results KNEC Portal KNEC Past Papers for Colleges Kasneb Past Papers KNEC Revision Papers KNEC Technical Exams Past Papers Kusoma Physics Notes Kusoma Physics Notes Pdf Kusoma Notes Physics Kusoma.co.ke Kusoma.com Past Papers Learner Guide for Cambridge IGCSE Physics Longhorn Physics Book 3 Pdf Made Familiar Physics Made Familiar Physics Pdf Made Familiar Physics Questions Maktaba Tetea Notes Marking Scheme KCSE Physics Past Papers Math Form2 Note Mcqs About Gaseous Exchange Middle School Physics Bowl Physics Questions Mock Past Papers 2017 Mock Past Papers With Answers Mokasa Mock 2017 More Than 1800 Physics Questions and Answers to Help You Study Multiple Choice Questions on Physics Necta Physics Past Papers Necta Physics Practicals Necta PhysicsPast Papers Necta PhysicsPracticals Necta Form Four Past Papers Necta Past Papers Form 4 Necta Past Papers Form 4 2016 Necta Past Papers Form Six Necta Past Papers Form Two Necta Questions and Answers Necta Review Questions Notes Physics Form 1 Notes Physics Form 2 Notes Physics Form 3 Notes Physics Form 3 Notes Pdf Notes Physics Form 3 Syllabus Notes Physics Form 4 Syllabus Notes on Physics Studies Notes Za Physics 4m 2 Notes Za Physics Form One Notes Za Physics Form Three O Level Physics Practical Experiments O Level Physics Questions and Answers Pdf Orm Three Physics Notes Page Navigation Papacambridge Physics IGCSE Papers KNEC KCSE Online Past Papers KNEC KCSE Results Past Papers Past KCSE Papers Past Paper Questions by Topic Physics Past Papers 2014 Past Papers in Kenya Pdf Physics Form 3 Pdf Physics Notes Pdf Physics Notes Form 1 Pdf Physics Notes Form 2 Pdf Physics Notes Form 3 Pdf Physics Notes Form 4 Pdf Physics Notes Form Four Pdf Physics Notes Form One Pdf Physics Notes Form Three Pdf Physics Notes Form Two Pdf Form 1 Physics Questions and Answers Pdf Form 2 Physics Questions and Answers Pdf Form 3 Physics Questions and Answers Pdf Form 4 Physics Questions and Answers Pdf Form Four Physics Questions and Answers Pdf Form One Physics Questions and Answers Pdf Form Three Physics Questions and Answers Pdf Form Two Physics Questions and Answers Pdf Free KCSE Past Papers and Marking Schemes Pdf" Revision Questions Physics Form 1 Practical Physics Experiments Pdf Practical Physics Question and Answer Pdf Pre Mocks 2018 Preliminary Physics Primary and Secondary Tillage Implements Ppt Pte KNEC Past Papers Questions and Answers Pdf Physics Form 1 Questions and Answers Pdf Physics Form 2 Questions and Answers Pdf Physics Form 3 Questions and Answers Pdf Physics Form 4 Questions and Answers Pdf Physics Form Four Questions and Answers Pdf Physics Form One Questions and Answers Pdf Physics Form Three Questions and Answers Pdf Physics Form Two Questions Based to Introduction to Physics Questions on Gaseous Exchange in Humans Questions on Introduction to Physics Questions to Ask in Physics Class Questions to Confuse Your Physics Teacher Quizlet Physics Test Quizlet Test Questions Qustions in Physics and Answers Revision Revision Physics Notes and Questions? Revision Quiz for Physics for Form Three S.1 Physics Questions S.2 Physics Questions S.3 Physics Questions S.4 Physics Questions Sample Essays on Betrayal in the City School Physics Notes Secondary Physics Notes Secondary Physics Notes Pdf Secondary PhysicsNotes Pdf Senior 1 Physics Notes Senior 2 Physics Notes Senior 3 Physics Notes Senior 4 Physics Notes Senior 5 Physics Notes Senior 6 Physics Notes Senior Five Physics Notes Senior Four Physics Notes Senior One Physics Notes Senior Six Physics Notes Senior Three Physics Notes Senior Two Physics Notes Simple Scientific Questions Smart Questions to Ask a Physics Teacher Snab Physics Revision Notes Southwest Mock Paper 2 2016 Physics Only Spm Physics Revision Notes Spm Notes Success Physics Spm Pdf Success PhysicsSpm Pdf Summary of Physics Form 3 Tahossa Past Papers To Motivate a Form 4 KCSE Student To Motivate a Form 4 Student Topical Revision Material Tricky Physics Questions and Answers Tricky Physics Questions for Adults Tricky Physics Questions With Answers Tricky Physics Quiz Questions Two Physics Revision Questions University Physics Volume 3 Openstax University Physics Volume 3 Pdf University Physics Volume 4 Pdf Ur Revision Guide IGCSE Physics What Are the Types of Gametes Working of Excretory System Www.Physics Form One Notes.com Www.Physics From One KLB.com Www.form 1 Physics.com Www.form 2 Physics.com Www.form 3 Physics.com Www.form 4 Physics.com Www.form Four Physics.com Www.form One Physics.com Www.form Three Physics.com Www.form Two Physics.com Www.kusoma Notes Www.kusoma Revision Materials Www.kusoma.co.ke Physics Notes Xtremepapers IGCSE Physics Year 11 Physics Z Notes Physics IGCSE Znotes as Physics Form 1 Summarized Notes For Phyics Form 2 Summarized Notes For Phyics Form 3 Summarized Notes For Phyics Form 4 Summarized Notes For Phyics Form 1 Summarized Notes For Physics Form 2 Summarized Notes For Physics Form 3 Summarized Notes For Physics Form 4 Summarized Notes For Physics 2018 KCSE PHYSICS PRACTICAL QUESTIONS Physics Paper One 2017 Physics Paper Two 2017 Physics Paper Three 2017 Physics Paper 1 2017 Physics Paper 2 2017 Physics Paper 3 2017 A Level Physics Questions and Answers Pdf All Physics Questions and Answers Pdf,ppt Physics Exam Questions and Answers Pdf Physics Multiple Choice Questions and Answers Pdf Physics Questions and Answers for High Schools Pdf Physics Notes Form 1-4 Pdf Free High School Notes Kenya Free Kcse Revision Notes General Physics Test Questions and Answers Pdf High School Physics Multiple Choice Questions and Answers Pdf Kcse Physics Revision Notes Pdf Kcse Revision Books Pdf Kcse Revision Notes Pdf Kenya Secondary School Notes Pdf Notes of Form 123 and 4 All Subject Physics Notes Form 1 Free Download Advice to KCSE Candidates Best Revision Books for KCSE How to Pass an Exam Successfully How to Pass KCSE 2018 How to Pass KCSE 2019 How to Pass KCSE Physics Paper How to Pass KCSE Physics How to Pass KCSE Physics How to Pass KCSE 2019 K.c.s.e Physics Paper 1 2017 KCSE 2019 Prediction KCSE Prediction 2019 KCSE Revision Tips KCSE Physics Paper 1 2018 KCSE Physics Paper 2 2018 KCSE Physics Past Papers Pdf KCSE Past Papers 2012 KCSE Past Papers 2017 Pdf KCSE Past Papers 2018 KCSE Past Papers of Physics Pp2 KCSE Physics Past Papers Pdf Physics KCSE Papers With Their Marking Schemes Physics Paper 1 and Answers KCSE 2017 Papers and Marking Scheme KCSE 2019 Papers and Marking Scheme KCSE Physics Paper 1 2018 KCSE Physics Paper 1 2019 KCSE Physics Paper 1 2019 Past Papers KCSE Physics Paper 2 2017 KCSE Physics Paper 2 2018 KCSE Physics Paper 2 2019 KCSE Physics Paper 2 2019 Past Papers KCSE Physics Paper 3 2019 Past Papers KCSE Physics Past Papers and Answers KCSE Marking Schemes Pdf KCSE Past Papers 2015 Marking Schemes KCSE Past Papers 2019 Marking Schemes KCSE Past Papers Physics Paper 1 2019 KCSE Past Papers Physics Paper 2 2019 KCSE Past Papers Physics Paper 3 2019 Past Papers KCSE Physics Paper 1 2019 Past Papers KCSE Physics Paper 2 2019 Past Papers KCSE Physics Paper 3 2019 4m1 Notes Viusasa 4m2 Notes Viusasa 4m3 Notes Viusasa 4m4 Notes Viusasa Download on Viusasa - Download Now for Free Elimu - Viusasa Elimu Library | Notes, Exams, Lesson Plans, Schemes Elimu Online High School Notes - Revision Materials for Kenyan Schools Https //www.viusasa.com/elimu Kenya Notes Viusasa Elimu Form 1 Notes Viusasa Elimu Form 2 Notes Viusasa Elimu Form 3 Notes Viusasa Elimu Form 4 Notes Viusasa Elimu Form Four Notes Viusasa Elimu Form One Notes Viusasa Elimu Form Three Notes Viusasa Elimu Form Two Viusasa Viusasa Education Viusasa Elimu Viusasa Elimu Class 6 Viusasa Elimu Form 1 Viusasa Elimu Form 1 Notes Viusasa Elimu Form 2 Viusasa Elimu Form 2 Notes Viusasa Elimu Form 3 Viusasa Elimu Form 3 Notes Viusasa Elimu Form 4 Viusasa Elimu Form 4 Notes Viusasa Elimu Form Four Viusasa Elimu Form Four Notes Viusasa Elimu Form One Viusasa Elimu Form One Notes Viusasa Elimu Form Three Viusasa Elimu Form Three Notes Viusasa Elimu Form Two Viusasa Elimu Form Two Notes Viusasa High School Notes - Revision Materials for Kenyan Schools Viusasa Notes Physics Mock Papers Physics Paper 1 2019 Physics Paper 1 Notes Physics Paper 1 Questions and Answers Physics Paper 1 Questions and Answers Pdf Physics Paper 2 Form 3 Physics Paper 2 Notes Physics Paper 2 Questions and Answers Pdf Physics Past Papers Physics Past Papers Pdf Physics Questions and Answers Pdf Physics Revision Questions and Answers Pdf Physics Revision Questions Pdf Common Exam Questions in Physics Paper 1 Common Exam Questions in Physics Paper 2 Common Test Questions in Physics Paper 1 Common Tested Questions in Physics Paper 1 Commonly Tested Questions in Physics Paper 1 K.c.s.e.Physics Questions and Answers KCSE 2019 Physics Paper 1 Marking Scheme KCSE 2019 Physics Paper 2 KCSE 2019 Physics Paper 2 Marking Scheme KCSE 2020 Prediction Questions and Answers KCSE Physics Paper 1 2019 KCSE Physics Paper 2 2016 KCSE Physics Paper 2 2017 KCSE Physics Paper 2 2018 KCSE Physics Paper 2 2019 KCSE Physics Questions and Answers Most Tested Questions in Physics Paper 1 Most Tested Questions in Physics Paper 2 Mostly Tested Questions in Physics Paper 1 Mostly Tested Questions in Physics Paper 2 A Level Physics Notes Uganda Pdf Download Buddo Junior School Holiday Work Physics Notes for a Level Pdf Physics Notes Form 1 Physics Notes Form 3 the Mole Physics Notes Form 4 Physics Notes O Level Physics Notes O Level Uganda Physics Notes O Level Uganda Pdf Physics Notes Pdf Download Physics Notes Form 3 Physics Notes Form 3 Physics Questions and Answers Form Three Physics Syllabus Pdf Gayaza High School Physics Notes Gayaza High School Physics Notes Pdf Gayaza High School Physics Past Papers Gayaza High School Physics Past Papers Answers Gayaza High School Physics Past Papers Questions and Answers Gayaza High School E Learning Gayaza High School Elearning Platform Gayaza High School Examinations Gayaza High School Holiday Work Gayaza High School Notes Gayaza High School Notes 2021 Gayaza High School Notes 2022 Gayaza High School Notes 2023 Gayaza High School Notes Pdf Gayaza Junior School E Learning Platform Gayaza Junior School Holiday Work Gayaza O Level Physics Notes Home › Gayaza High School | Elearning Platform Kabojja Junior School Holiday Work Pdf Klb Physics Book 3 Klb Physics Form 3 Teachers Guide Klb Physics Notes List of Ugandan E-learning Platforms for Students Mirembe Junior School Holiday Work Ntare School Past Papers O Level Physics Notes Free Download O Level Physics Notes in Uganda O Level Physics Notes Pdf O Level Physics Notes Uganda Pdf O Level Physics Notes Uganda Pdf Download O Level General - Home › Gayaza High School | Elearning S.1 Physics Notes | Standard High School Zzana S.3 Physics Notes S.4 Physics 2 Notes | Standard High School Zzana Seeta High School Elearning Seeta High School Holiday Work Seeta High School Notes Seeta High School Notes Pdf Seeta High School Past Papers Seeta High School Past Papers Pdf Senior 1 Physics Notes Senior 1 Physics Notes in Uganda Senior 1 Physics Notes Uganda Senior 1 Physics Questions Senior 1 Exams Senior 1 Work Senior 1 Work 2020 Senior 1 Work 2020 Uganda Senior 2 Physics Notes Senior 2 Physics Notes in Uganda Senior 2 Physics Notes Uganda Senior 2 Physics Questions Senior 2 Exams Senior 2 Work Senior 2 Work 2020 Senior 2 Work 2020 Uganda Senior 3 Physics Notes Senior 3 Physics Notes in Uganda Senior 3 Physics Notes Uganda Senior 3 Physics Questions Senior 3 Exams Senior 3 Work Senior 3 Work 2020 Senior 3 Work 2020 Uganda Senior 4 Physics Notes Senior 4 Physics Notes in Uganda Senior 4 Physics Notes Uganda Senior 4 Physics Questions Senior 4 Exams Senior 4 Work Senior 4 Work 2020 Senior 4 Work 2020 Uganda Senior Four Physics Notes Senior Four Physics Notes in Uganda Senior Four Physics Notes Uganda Senior Four Physics Questions Senior Four Exams Senior Four Work Senior Four Work 2020 Senior Four Work 2020 Uganda Senior One Physics Notes Senior One Physics Notes in Uganda Senior One Physics Notes Uganda Senior One Physics Questions Senior One Exams Senior One Work Senior One Work 2020 Senior One Work 2020 Uganda Senior Three Physics Notes Senior Three Physics Notes in Uganda Senior Three Physics Notes Uganda Senior Three Physics Questions Senior Three Exams Senior Three Work Senior Three Work 2020 Senior Three Work 2020 Uganda Senior Two Physics Notes Senior Two Physics Notes in Uganda Senior Two Physics Notes Pdf Senior Two Physics Notes Uganda Senior Two Physics Questions Senior Two Exams Senior Two Work Senior Two Work 2020 Senior Two Work 2020 Uganda St Mary's Kitende E Learning Standard High School Notes Standard High School Zana a Level Notes Standard High School Zana Com Notes Standard High School Zana E Learning Standard High School Zana E Learning Platform Standard High School Zana E-learning Platform Standard High School Zana Notes for Senior Two Standard High School Zana Notes Pdf Standard High School Zana Website Standard High Zana Notes Uace Physics Notes Uace Physics Notes Pdf Uce Physics Notes Pdf Uce Physics Notes Pdf Download Uce Past Papers Uganda Secondary Schools E-learning Platform Uneb Marking Guides Pdf Uneb Past Papers and Answers Pdf Physics Form 1 Questions and Answers Pdf Download Physics Notes Form 1-4 Physics Form 1 Questions and Answers Pdf Form 1 Physics Topical Questions Form 1 Physics Exam Paper With Answer Pdf Form 1 Exams 2020 Form 1 Exams 2021 Form 1 Exams 2022 Form 1 Exams 2023 Form 1 Physics Past Papers Form 1 Physics Revision Papers With Answers Sample Physics Test for Form One Exams Ntare School Past Papers Seeta High School Notes Pdf Seeta High School Past Papers Seeta High School Past Papers Pdf St Mary's Kitende Past Papers Uce Physics Notes Pdf Uce Past Papers Uneb Marking Guides Pdf Uneb Past Papers and Answers Pdf Physics Book 3 Download Physics Form 3 Questions and Answers Physics Form 3 Syllabus Physics Form 3 Topics Physics Notes Form 3 Physics Notes Form 3 Physics Notes Form 3 Physics Notes Form Three Physics Notes Pdf Download Form 3 Physics Exam Form 3 Physics Notes on Pdf Revision Physics Revision a Level Physics Revision Notes - Physics S.1-Physics-notes S.1-Physics-notes Uganda S.2-Physics-notes S.2-Physics-notes Uganda S.3-Physics-notes S.3-Physics-notes Uganda S.4-Physics-notes S.4-Physics-notes Uganda S.5-Physics-notes S.5-Physics-notes Uganda S.6-Physics-notes S.6-Physics-notes Uganda S1 Physics Notes Term 1 S1 Physics Notes Term 2 S1 Physics Notes Term 3 S2 Physics Notes Term 1 S2 Physics Notes Term 2 S2 Physics Notes Term 3 S3 Physics Notes Term 1 S3 Physics Notes Term 2 S3 Physics Notes Term 3 S4 Physics Notes Term 1 S4 Physics Notes Term 2 S4 Physics Notes Term 3 Senior 3 Physics Notes Senior 3 Physics Notes Uganda Senior Three Physics Notes Senior Three Physics Notes Uganda Physics Form 1 the Cell Physics Form One Notes Free – Education News Physics Notes Form 1-4 Physics Questions and Answers Form 1 - Physics Form One Physics Questions and Answers Form 2 - Physics Form Two Physics Questions and Answers Form 3 - Physics Form Three Physics Questions and Answers Form 4 - Physics Form Four Physics Questions and Answers Senior 1 - Physics Senior One Physics Questions and Answers Senior 2 - Physics Senior Two Physics Questions and Answers Senior 3 - Physics Senior Three Physics Questions and Answers Senior 4 - Physics Senior Four Physics Topic by Topic Questions and Answers Combined Science Notes Form 1 Form 1 Physics Revision Questions and Answers Form 1 Physics Topical Questions Form 1 Revision Papers With Answers Form 2 Physics Revision Questions and Answers Form 3 Physics Revision Questions and Answers Form Four Physics Revision Questions and Answers Form One Physics Revision Questions and Answers Form Three Physics Revision Questions and Answers Form Two Physics Revision Questions and Answers Free Physics Form 1 Notes Free Physics Notes Introduction to Physics Form One Kcse Past Papers: Physics Form 1 Kcse Past Papers: Physics Form 1 Topical Questions Kcse Past Papers: Physics Form 1 Topical Questions and Answers Most Tested Areas in Physics Kcse Most Tested Areas in Physics Kcse Exams Most Tested Areas in Physics Uneb Most Tested Areas in Form 1 in Physics Most Tested Areas in Form 2 in Physics Most Tested Areas in Form 3 in Physics Most Tested Areas in Form 4 in Physics Most Tested Areas in Form Four in Physics Most Tested Areas in Form One in Physics Most Tested Areas in Form Three in Physics Most Tested Areas in Form Two in Physics Most Tested Areas in Kcse Physics Most Tested Areas in Kcse Physics Exams Most Tested Areas in Senior 1 in Physics Most Tested Areas in Senior 2 in Physics Most Tested Areas in Senior 3 in Physics Most Tested Areas in Senior 4 in Physics Most Tested Areas in Senior Four in Physics Most Tested Areas in Senior One in Physics Most Tested Areas in Senior Three in Physics Most Tested Areas in Senior Two in Physics Most Tested Areas in Uneb Physics Revision Notes Physics Form 1 - Free Kcse Past Papers Who Was Physics Champion KCSE 2019 Top 100 Students in Physics KCSE 2019 Best 100 Students in Physics KCSE 2019 Top Student in Physics KCSE Best Student in Physics KCSE Who Was Physics Champion KCSE 2020 Top 100 Students in Physics KCSE 2020 Best 100 Students in Physics KCSE 2020 Names of Best Physics Students KCSE Names of Top Physics Students KCSE High School Physics Notes Pdf Klb Physics Form 1 Book Pdf Physics Form 1 Best Notes Physics Form 1 Notes Pdf Physics Form 1 Pressure Physics Form 1 Questions and Answers Physics Form 1 Questions and Answers Pdf Download Physics Form 2 Best Notes Physics Form 3 Best Notes Physics Form 4 Best Notes Physics Form Four Best Notes Physics Form One Best Notes Physics Form Three Best Notes Physics Form Two Best Notes Physics Notes Form 1 to 4 Physics Notes Pdf Klb Physics Form 1 Book Pdf Physics Form 1 Notes Pdf Physics Form 1 Pressure Physics Form 1 Questions and Answers Physics Form 1 Questions and Answers Pdf Download Physics Notes Form 1-4 Pdf Physics Notes Pdf Physics Summary Notes Pdf

Army Jobs - Navy Jobs - Military Jobs

Scholarship 2024/25

Current Scholarships 2024/2025 - Fully Funded

Full Undergraduate Scholarships 2024/2025

Fully Funded Masters Scholarships 2024/25

PhD Scholarships for International Students - Fully Funded!

Funding Opportunities for Journalists 2024/2025

Funding for NGOs 2024/2025

Funding for Artists 2024/2025

Funding for Entrepreneurs 2024/2025

✅Over 4500 Current Fully Funded Scholarships for International Students

✅ Undergraduate Scholarships 2024

✅ Masters Scholarships 2024

✅ PhD Scholarships 2024 Click Here!

Army Jobs - Navy Jobs - Military Jobs

Scholarship 2024/25

Current Scholarships 2024/2025 - Fully Funded

Full Undergraduate Scholarships 2024/2025

Fully Funded Masters Scholarships 2024/25

PhD Scholarships for International Students - Fully Funded!

Funding Opportunities for Journalists 2024/2025

Funding for NGOs 2024/2025

Funding for Artists 2024/2025

Funding for Entrepreneurs 2024/2025

✅Over 4500 Current Fully Funded Scholarships for International Students

✅ Undergraduate Scholarships 2024

✅ Masters Scholarships 2024

✅ PhD Scholarships 2024 Click Here!

Free Scholarship Newsletter --- E-mail Address

First Name

Then Don't worry — your e-mail address is totally secure. I promise to use it only to send you Advance Africa Newsletter.