KCSE Past Papers Maths B 2013
Click Here - Free KCSE Past Papers » KNEC Past Exams » Free Downloads » KCSE Papers & Marking Schemes
Mathematics Alt. B Paper 1 (122/1)
SECTION 1 (50 marks)
Answer all questions in this section in the spaces provided.
1.Without using a calculator, evaluate:
-3(-5 — + 7) + 2(-3 + +6).
2. The first four prime numbers are written in descending order to form a number.
(a) Write down the number.
(b) Find the total value of the hundreds digit in the numbers,
3. Without using a calculator evaluate:(3 marks)
4. Tito owned Ksh 600 to Nekesa, Ksh 750 to Mwita and Ksh 650 to A uma. He had Ksh 1200 to repay to the three people in proportion to what he owed them. Calculate the amount of money Mwita rcceived more than Nekesa. (3 marks)
5. Given that r — 2 and h = 3r — 1, evaluate 7r2 + 2rh/√ 4h - 2r (3 marks)
6. The surface area of a cube is 1176 cm3. Determine the length of one of” its sides. (3 marks)
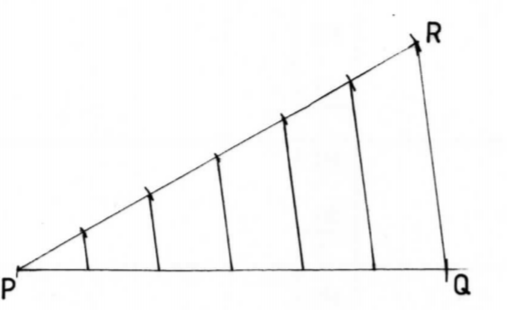
7. By construction, divide the line PQ below into six equal parts. (3 marks)

9.A box contains Cve shillings coins and ten shillings coins. The number of ten shillings coins are 6 times as many as the five shillings coins.
The total value ot’all the coins in the box is Ksh 2600. Determine the total number of coins in the box. (4 marks)
10. Simplify 3-2 x 813/2/4-3 ÷ 81/3
leaving your answer in index form. Hence evaluate the expression. (4 marks)
11. A retailer bought a mobile phone for Ksh 5750. The marked price at the retailer’s shop was 12% higher than the buying price.
After allowing a certain discount, the retailer sold the mobile phone for Ksh 6118. Calculate the percentage discount. (3 marks)
12. Factorise 9a2 — 16/b2c2
(2 marks)
13. Three types of books A, B and C were each piled on a table to attain the same height. The thickness of the books were 12 mm, 28 mm and 54 mm for types A, B and C respectively. Find:
(a) the least height attained;
(b) the number of type A books piled. (3 marks)
14. The sum of the interior angles of a regular polygon is 1260°. Find the size of each interior angle. (3 marks)
15. The corresponding lengths of two similar triangles are 5 cm and 7.5 cm. If the area of the larger triangle is 22.5 cm2, calculate the area of the smaller triangle. (3 marks)
16. The area of a sector of a circle is 77 cm2'. The arc of the sector subtends an angle of 45° at the centre of the circle. Find the circumference of the circle. (Take ℿ=22/7 (4 marks)
SECTION II (50 marks)
Answer only Ave questions in this section in the spaces provided.
17. The figum below represents a solid prism with a semi-circular groove. The dimensions are as shown.
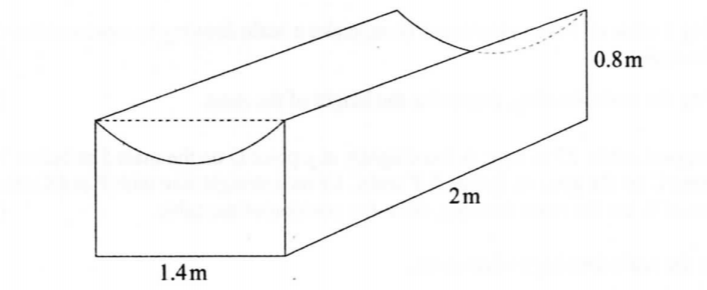
(i) the volume of the prism;
(ii) the total surface area of the prism. (4 marks)
(b) All the rectangular faces are painted. Calculate the percentage of the surface of the prism that is painted correct to 1 decimal place. (2 marks)
18. (a) Three vertices of a parallelogram ABCD are A(—7, 3), B( 1. — I) and C(5, 1). On the grid provided, draw the parallelogram ABCD.
(b) Determine:
(i) the gTadient of the line AB; (2 marks)
(ii) the equation or line AB in the form y = m.r + c, where m and c are constants. (2 marks)
(c) Another line L is perpendicular to CD and passes through point (1, 3). Determine:
(i) the equation of L in the form ax + by = c where a, b and c are constants; (3 marks)
(ii) the coordinates of the y-intercept of line L. (1 mark)
19. (a) The roots of a quadratic equation are 2 and — 1. Write down the quadratic equation in the form ar° + bx + c = 0, where a, b and c are integers. (3 marks)
(b) (i) Barasa bought (2y + l ) mangoes at y shillings each. The total cost of the mangoes was Ksh 55. Find the cost of each mango. (4 marks)
(ii) Karau spent Ksh 95 more than Barasa to buy the same type of mangoes. For every 6 mangoes he bought, he was given one extra mango. Calculate the total number of mangoes Karau got. (3 marks)
20. The angle of elevation of the top T, of a vertical mast from a point P, 100 m away from the foot F, o(the mast is 14°.
(a) Using a scale of l cm to represent 10 m, make a scale drawing to represent the above information. (3 marks)
(b) Using the scale drawing, determine the height of the mast. (2 marks)
(c) A support cable, 27 m long, is fixed tightly at a point D on the mast 5 m below T and at a point C on the ground. Points P, F and C lie on a straight line with P and C on opposite sides ot’ F. On the scale drawing, show the position of the cable. (2 marks)
(d) Use the scale drawing to determine:
(i) the angle of depression of C from D; (1 marks)
(ii) the distance of C from P. (2 marks)
21. ln the figure below, P, Q, R and S are points on the circumference of the circle centre O.
TP and TR are tangents to the circle at P and R respectively. POQ is a diameter of the circle and angle PQR = 64°.
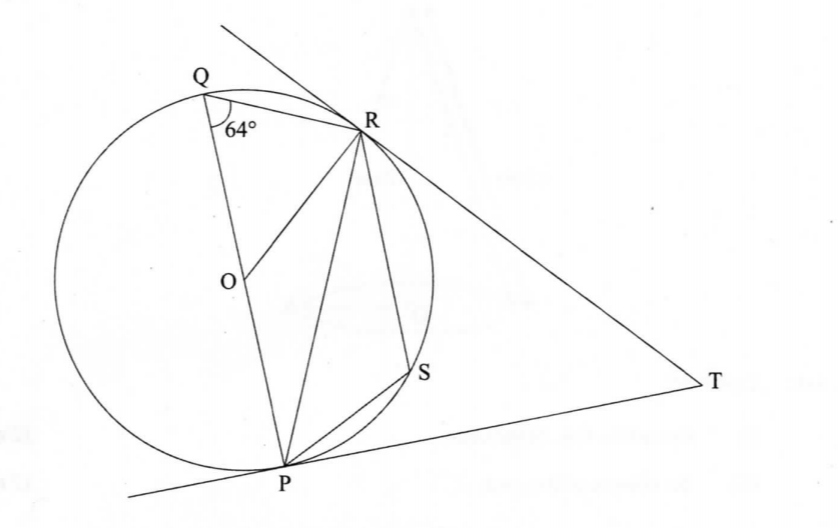
(a) ∠ ROP; (2 marks)
(b) ∠ PSR; (2 marks)
(c) ∠ ORP; (2 marks)
(d) ∠ RP; (2 marks)
(e) ∠RTP. (2 marks)
22. The figurc below represents a cone whose vertical height is 12 cm and slant hcight is 13 cm.
(a) Calculate:
(i) the radius, OA. of the cone; (2 marks)
(ii) the volume of the cone. (2 marks)
(b) A smaller cone of radius 6 cm is cut off’ from the com: alx» c to leave a i?ustum. Calculate:
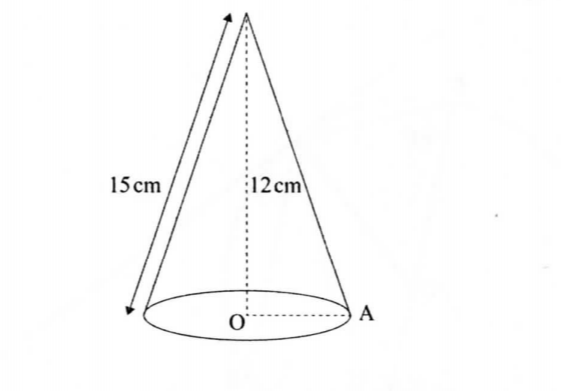
(ii) the volume of the smaller cone:
(iii) the volumc of the frustrum.
23. The vertices of a trapezium ABCD are A(2, 0), B(4, 0), C(6, 2) and D(2, 2).
(a) On the grid provided below, draw:
(i) the trapezium ABCD; (1 mark)
(iii) A”B”C“D“ the image of A’B'C’D’ under a rotation of —90°, centre (0, 0). (2 marks)
(b) Describe a transformation that maps A"B“C”D” onto ABCD. (2 marks)
(c) State pairs of trapezia that are directly congruent and those that are oppositely congruent. (3 marks)
24. A racing motorcycle started from rest and moved with a constant acceleration ot” 1 m/s2for 15 seconds. lt then accelerated at 3.5 m/s2 for the next 10 seconds and maintained a constant speed for the next 10 seconds. It decelerated constantly and came to rest after 25 seconds.
(a) On the grid provided, draw the velocity—time graph for the motorcycle. (4 marks)
(b) Use the graph to determine:
(i) the deceleration of the motorcycle; (2 marks)
(ii) the total distance travelled; (2 marks)
(iii) the average speed for the motorcycle, correct to 3 significant figures. (2 marks)
Questions and Answers Mathematics ALT. B (I22) 2013
1.Without using a calculator, evaluate:
-3(-5 — + 7) + 2(-3 + +6).

(a) Write down the number.
7532
(b) Find the total value of the hundreds digit in the numbers,
Total Value of hundreds digit = 500
3. Without using a calculator evaluate:(3 marks)
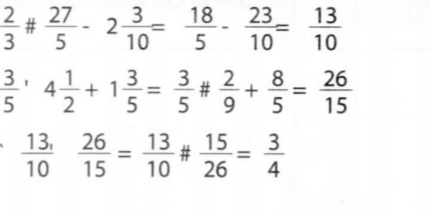

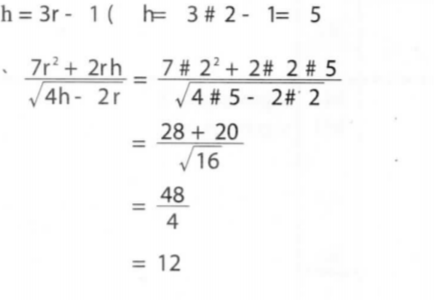
Area of each face = 1176/6 =196 Lenght of one side √ 196 =14
7. By construction, divide the line PQ below into six equal parts. (3 marks)

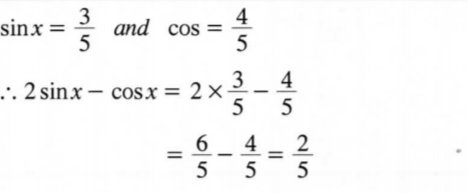
The total value ot’all the coins in the box is Ksh 2600. Determine the total number of coins in the box. (4 marks)

leaving your answer in index form. Hence evaluate the expression. (4 marks)
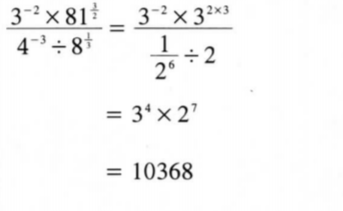
After allowing a certain discount, the retailer sold the mobile phone for Ksh 6118. Calculate the percentage discount. (3 marks)

(2 marks)
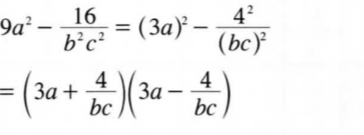
(a) the least height attained;

Number of books = 756/12 =63
14. The sum of the interior angles of a regular polygon is 1260°. Find the size of each interior angle. (3 marks)

15. The corresponding lengths of two similar triangles are 5 cm and 7.5 cm. If the area of the larger triangle is 22.5 cm2, calculate the area of the smaller triangle. (3 marks)
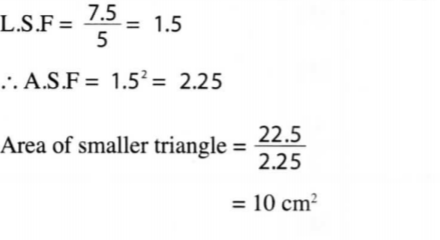

Answer only five questions in this section in the spaces provided.
17. The figum below represents a solid prism with a semi-circular groove. The dimensions are as shown.

(i) the volume of the prism;
(ii) the total surface area of the prism. (4 marks)
(b) All the rectangular faces are painted. Calculate the percentage of the surface of the prism that is painted correct to 1 decimal place. (2 marks)

(i) the gradient of the line AB; (2 marks)
(ii) the equation or line AB in the form y = m.r + c, where m and c are constants. (2 marks)
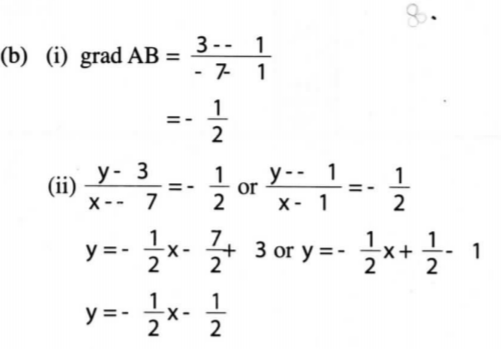
(i) the equation of L in the form ax + by = c where a, b and c are constants; (3 marks)
(ii) the coordinates of the y-intercept of line L. (1 mark)

(b) (i) Barasa bought (2y + l ) mangoes at y shillings each. The total cost of the mangoes was Ksh 55. Find the cost of each mango. (4 marks)
(ii) Karau spent Ksh 95 more than Barasa to buy the same type of mangoes. For every 6 mangoes he bought, he was given one extra mango. Calculate the total number of mangoes Karau got. (3 marks)
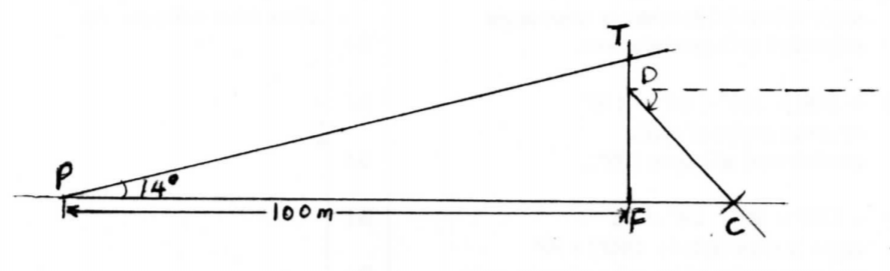
(b) Using the scale drawing, determine the height of the mast. (2 marks)
Height of mat → 2.5± 0.1
=2.5x10
=25m
(c) A support cable, 27 m long, is fixed tightly at a point D on the mast 5 m below T and at a point C on the ground. Points P, F and C lie on a straight line with P and C on opposite sides ot’ F. On the scale drawing, show the position of the cable. (2 marks)
Position of cale drawn (d) Use the scale drawing to determine:
(i) the angle of depression of C from D; (1 marks)
∠ of depression of c from D 48 ∘ ±+ 1∘
(ii) the distance of C from P. (2 marks)
(10+1.8∘ 1.8 .1)x10
=118 ∘ 1m
21. ln the figure below, P, Q, R and S are points on the circumference of the circle centre O.
TP and TR are tangents to the circle at P and R respectively. POQ is a diameter of the circle and angle PQR = 64°.

(a) ∠ ROP; (2 marks)
+ ROP = 2 4 64' = 1 28' angle subtended at centre is twice angle subtended at O circumference,
(b) ∠ PSR; (2 marks)
(b) -r PSR = 180”- 64’ = 116°
opposite angles of cyclic quadrilateral add up to 180°.
(c) ∠ ORP; (2 marks)
+ ORP = 90‘ - 64‘ =• 26‘
angle in semicircle (+ QRP) = 90° and base angles of isosceles triangle equal.
(d) ∠ RP; (2 marks)
+ TRP = 64° angle in alternate segment.
(e) ∠RTP. (2 marks)
+ RTP = 180 - 2 ^64 h= 52° + TRP = 64° angle in alternate segment and sum of angles in triangle PRT = 180°.
22. The figurc below represents a cone whose vertical height is 12 cm and slant hcight is 13 cm.
(a) Calculate:
(i) the radius, OA. of the cone; (2 marks)
(ii) the volume of the cone. (2 marks)
(b) A smaller cone of radius 6 cm is cut off’ from the com: alx» c to leave a frustrum. Calculate:

(ii) the volume of the smaller cone:
(iii) the volumc of the frustrum.

(a) On the grid provided below, draw:
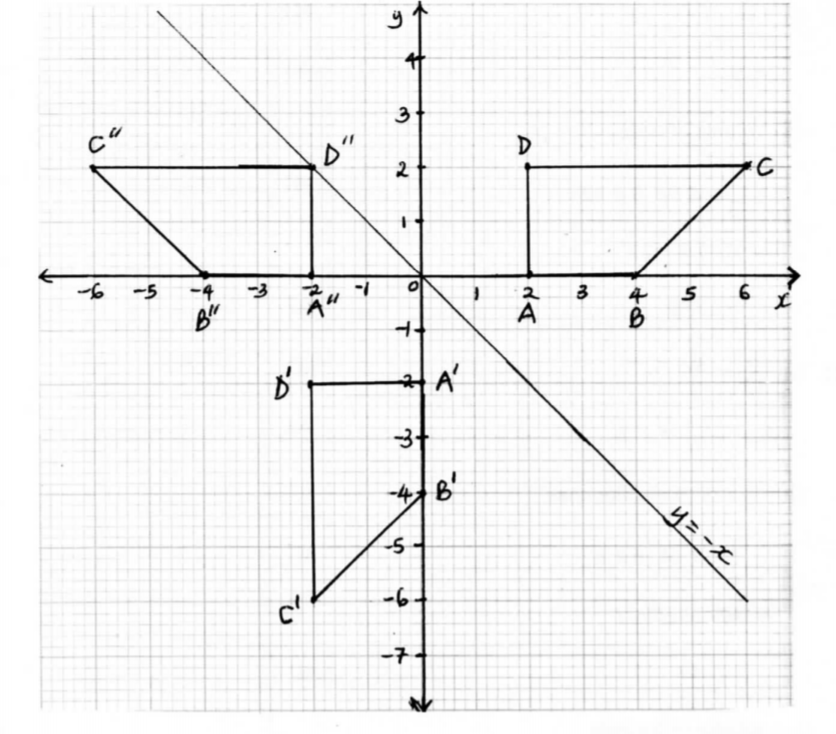

(ii) line of reflection y = — x drawn trapezium A'B'C'D'drawn
(iii) A”B”C“D“ the image of A’B'C’D’ under a rotation of —90°, centre (0, 0). (2 marks)
points A"B"C"D" plotted trapezium A"B"C"D" drawn
(b) Describe a transformation that maps A"B“C”D” onto ABCD. (2 marks)
(b) transformation which maps A"B"C"D" onto ABCD reflection on line x = 0
(c) State pairs of trapezia that are directly congruent and those that are oppositely congruent.(3 marks)
(c) directly congruent pair A'B'C'D' and A"B"C"D" oppositely congruent pairs ABCD and A'B'C'D' ABCD and A"B"C"D"
24. A racing motorcycle started from rest and moved with a constant acceleration ot” 1 m/s2for 15 seconds. lt then accelerated at 3.5 m/s2 for the next 10 seconds and maintained a constant speed for the next 10 seconds. It decelerated constantly and came to rest after 25 seconds.
(a) On the grid provided, draw the velocity—time graph for the motorcycle. (4 marks)

(i) the deceleration of the motorcycle; (2 marks)
deceleration = 50/25 = 2 mls2
(ii) the total distance travelled; (2 marks)
Total distance = ( 15 x 15) + 2( 15 + 50) x 10 + 10 x 50 + 1 (25x50) = 112.5 + 325 + 500 + 625 = 1562.5
(iii) the average speed for the motorcycle, correct to 3 significant figures. (2 marks)
Average speed = 1562.5 /60
= 26.0416 = 26.0 m/s2
Kenya Scholarships for Undergraduate Students » Kenya Scholarships for Postgraduate Students » Undergraduate Scholarships for Kenyan Students » Kenya Undergraduate Scholarships » Full Undergraduate Scholarships for Kenyans » Kenya Postgraduate Scholarships » Scholarships & Grants » Undergraduate Scholarships » Universities in Kenya » Kenya Universities and Colleges Central Placement Service (KUCCPS) » Colleges in Kenya » KASNEB Registration & Results » Secondary Schools Scholarships in Kenya » Undergraduate & Graduate Scholarships for Kenyans
Scholarships for African Students » Undergraduate Scholarships » African Women Scholarships & Grants » Developing Countries Scholarships » Erasmus Mundus Scholarships for Developing Countries » Fellowship Programs » Funding Grants for NGOs » Government Scholarships » LLM Scholarships » MBA Scholarships » PhD and Masters by Research Scholarships » Public Health Scholarships - MPH Scholarships » Refugees Scholarships » Research Grants » Scholarships and Grants
Scholarships in Australia » Scholarships in Belgium » Scholarships in Canada » Scholarships in Germany » Scholarships in Italy » Scholarships in Japan » Scholarships in Korea » Scholarships in Netherlands » Scholarships in UK » Scholarships in USA "Pdf" Revision Questions Mathematics Form 1 "Pdf" Revision Questions Mathematics Form 2 "Pdf" Revision Questions Mathematics Form 3 "Pdf" Revision Questions Mathematics Form 4 "Pdf" Revision Questions Mathematics Form Four "Pdf" Revision Questions Mathematics Form One "Pdf" Revision Questions Mathematics Form Three "Pdf" Revision Questions Mathematics Form Two 1 a a KCSE Past Papers 10th Grade Mathematics Questions and Answers 10th Grade Mathematics Test 11th Ncert Mathematics 12th Class Mathematics Book Free Download 2014 KCSE Marking Schemes 2014 Pdf KCSE Past Papers 2015 2015 Mathematics Essay Questions and Answers Form 4 2016 KCSE Papers 2016 KCSE Prediction Questions 2017 Mathematics Hsc Answers 2017 KCSE Prediction Questions 2018 Mathematics KCSE Leakage 2018 Mathematics KCSE Questions 2018 KCSE Busineness Studies 2018 KCSE Exam 2018 KCSE Leakage 2018 KCSE Prediction Questions 2018 KCSE Questions 2019 Mathematics KCSE Leakage 2019 Mathematics KCSE Questions 2019 KCSE Leakage 2019 KCSE Questions 9th Grade Mathematics Study Guide A a a Mathematics Notes a a a Mathematics Notes! a a a MathematicsNotes! A a KCSE Past Papers A Biblical View of Social Justice A Level Mathematics Biological Molecules Questions A Level Mathematics Exam Questions by Topic A Level Mathematics Notes Edexcel A Level Mathematics Notes Xtremepapers A Level Mathematics Past Papers A Level Mathematics Questions and Answers a Level Mathematics Questions and Answers A Level Mathematics Questions and Answers (Pdf) A Level Mathematics Questions and Answers Pdf A Level Mathematics Questions by Topic Kidney Questions With Markschemes A Level Mathematics Revision A Level Mathematics Revision Edexcel A Level Mathematics Revision Guide A Level Mathematics Revision Notes A Level Mathematics Revision Notes Pdf A Level Mathematics Textbook Pdf A Level Mathematics Year 1 / as Aqa Exam Questions by Topic A Level Edexcel Notes a* Mathematics aa Mathematics Form 3 Questions and Answers Advance KCSE Past Papers Advance-africa.com KCSE Rev Quiz Advantages and Disadvantages. All Mathematics Essays All Mathematics Notes for Senior Two All KCSE Past Papers Mathematics With Making Schemes All Marking Schemes Questions and Answers All Past K.c.s.e Questions With Answers Alliance Mocks 2017 Ap Bio Quizzes Ap Mathematics 1 Textbook Pdf Ap Mathematics Essay Questions and Answers Are Sourced From KNEC. As Level Mathematics Notes Atika Mathematics Notes Atika School Mathematics Notes B/s Book 2 Notes Basic Mathematics Books Pdf basic Mathematics Interview Questions and Answers Pdf Basic Mathematics Interview Questions and Answers Pdf Basic Mathematics Pdf Basic Mathematics Questions and Answers Basic Mathematics Questions and Answers Pdf Bbc Bitesize Mathematics Ks3 Bihar Board Mathematics Objective Answer 2017 Bihar Board Mathematics Objective Answer 2018 Bio Answers Bio Quesions Mathematics 0478 Mathematics 101 Mathematics 12th Mathematics 12th Class Notes Pdf Mathematics 2019 Syllabus Mathematics All KCSE Short Notes Mathematics Answers Mathematics Answers Online Free Mathematics Answers Quizlet Mathematics Bk 2 Notes Mathematics Book 1 Mathematics Book 1 Notes Mathematics Book 2 Mathematics Book 2 Notes Mathematics Book 3 Mathematics Book 3 KLB Mathematics Book 3 Notes Mathematics Book 4 Mathematics Book 4 Notes Mathematics Book 4 Pdf Mathematics Book for Class 11 Mathematics Book Four Mathematics Book Four Notes Mathematics Book One Mathematics Book One Notes Mathematics Book Pdf Free Download Mathematics Book Three Mathematics Book Three Notes Mathematics Book Three Pdf Mathematics Book Two Mathematics Book Two Notes Mathematics Books Form Three Mathematics Bowl Mathematics Study Guide Mathematics Bowl Questions Mathematics Mathematics Bowl Questions Earth Mathematics Mathematics Bowl Questions Math Mathematics Bowl Questions Middle School Mathematics Brekthrough Form Two Notes Mathematics Class 12 Ncert Solutions Mathematics Class 12 Pdf Mathematics Communication Syllabus Mathematics Diagram Software Mathematics Diagrams for Class 11 Mathematics Diagrams for Class 12 Mathematics Diagrams for Class 9 Mathematics Diagrams for Class-10 Mathematics Diagrams in Form 1 Mathematics Diagrams in Form 2 Mathematics Diagrams in Form 3 Mathematics Diagrams in Form 4 Mathematics Diagrams Pdf Mathematics Diagrams to Label Mathematics Essay Questions and Answers Mathematics Essay Questions and Answers 2018 Mathematics Essay Questions and Answers Form 1 Mathematics Essay Questions and Answers Form 2 Mathematics Essay Questions and Answers Form 3 Mathematics Essay Questions and Answers Form 4 Mathematics Essay Questions and Answers Form 4 Pdf Mathematics Essay Questions and Answers Pdf Mathematics Essay Revision Q Mathematics Essays and Answers Mathematics Essays Form One to Form Four Mathematics Essays Form One to Form Three Mathematics Essays KCSE Mathematics Essays Pdf Mathematics Exam 1 Multiple Choice Mathematics Exam 2 Advance Mathematics Exam 2 Test Mathematics Exam 2016 Mathematics Exam Form Four Mathematics Exam Form One Mathematics Exam Form Three Mathematics Exam Form Two Mathematics Exam Practice Test Mathematics Exam Questions Mathematics Exam Questions and Answers Mathematics Exam Questions and Answers Pdf Mathematics Exam Study Guide Mathematics Exams Mathematics Excretion Notes Mathematics Exercise Form 4 With Answers Mathematics Final Exam Answer Key Mathematics Final Exam Answer Key 2016 Mathematics Final Exam Answer Key 2017 Mathematics Final Exam Answers 2018 Mathematics Final Exam Answers 2019 Mathematics Final Exam Questions and Answers Mathematics Fom 1 Notes Mathematics Fom 2 Notes Mathematics Fom 3 Notes Mathematics Fom 4 Notes Mathematics Form 1 Mathematics Form 1 & 2 and Answers Mathematics Form 1 and 2 Essays Mathematics Form 1 and 2 Essays Questions and Answers Mathematics Form 1 Chapter 1 Mathematics Form 1 Diagrams Mathematics Form 1 Exams Mathematics Form 1 Mid Year Exam Mathematics Form 1 Notes Mathematics Form 1 Notes and Questions Mathematics Form 1 Notes Download Mathematics Form 1 Notes Free Download Mathematics Form 1 Notes GCSE Mathematics Form 1 Notes KCSE-kcse Mathematics Form 1 Notes Pdf Mathematics Form 1 Notes Pdf Download Mathematics Form 1 Past Papers Mathematics Form 1 Pdf Mathematics Form 1 Pressure Mathematics Form 1 Question Papers Mathematics Form 1 Questions Mathematics Form 1 Questions and Answers Mathematics Form 1 Questions and Answers Pdf Mathematics Form 1 Quiz Mathematics Form 1 Revision Questions Mathematics Form 1 Summary Notes Mathematics Form 1 Syllabus Mathematics Form 1 Work Mathematics Form 1-4 Notes Mathematics Form 2 Mathematics Form 2 Chapter 1 Mathematics Form 2 Chapter 2 Mathematics Form 2 Diagrams Mathematics Form 2 Exam Paper 2014 Mathematics Form 2 Exams Mathematics Form 2 Notes Mathematics Form 2 Notes and Questions Mathematics Form 2 Notes GCSE Mathematics Form 2 Notes KCSE-kcse Mathematics Form 2 Notes Pdf Mathematics Form 2 Notes Pdf Download Mathematics Form 2 Past Papers Mathematics Form 2 Pdf Mathematics Form 2 Question Papers Mathematics Form 2 Questions Mathematics Form 2 Questions and Answers Mathematics Form 2 Questions and Answers Pdf Mathematics Form 2 Quiz Mathematics Form 2 Revision Notes Mathematics Form 2 Salts Mathematics Form 2 Structure and Bonding Mathematics Form 2 Summary Notes Mathematics Form 2 Syllabus Mathematics Form 2 Work Mathematics Form 3 Mathematics Form 3 and 4 Essays Mathematics Form 3 and 4 Essays Questions and Answers Mathematics Form 3 Chapter 3 Mathematics Form 3 Classification Mathematics Form 3 Diagrams Mathematics Form 3 Ecology Mathematics Form 3 Exams Mathematics Form 3 Notes Mathematics Form 3 Notes and Questions Mathematics Form 3 Notes GCSE Mathematics Form 3 Notes KCSE-kcse Mathematics Form 3 Notes Pdf Mathematics Form 3 Notes Pdf Download Mathematics Form 3 Notes Topic 1 Mathematics Form 3 Past Papers Mathematics Form 3 Pdf Mathematics Form 3 Question Papers Mathematics Form 3 Questions Mathematics Form 3 Questions and Answers Mathematics Form 3 Questions and Answers Pdf Mathematics Form 3 Questions and Answers Term 3 Mathematics Form 3 Questions and Answers+pdf Mathematics Form 3 Quiz Mathematics Form 3 Revision Notes Mathematics Form 3 Revision Questions Mathematics Form 3 Summary Notes Mathematics Form 3 Syllabus Mathematics Form 3 Syllabus Pdf Mathematics Form 3 Topics Mathematics Form 3 Work Mathematics Form 4 Mathematics Form 4 All Chapter Mathematics Form 4 Chapter 1 Conversion of Units Mathematics Form 4 Chapter 1 Exercise Mathematics Form 4 Chapter 1 Exercise and Answers Mathematics Form 4 Chapter 1 Exercise Pdf Mathematics Form 4 Chapter 1 Mind Map Mathematics Form 4 Chapter 2 Mathematics Form 4 Chapter 2 Exercise and Answers Mathematics Form 4 Chapter 2 Exercise Pdf Mathematics Form 4 Chapter 2 Experiment Mathematics Form 4 Chapter 2 Formula Mathematics Form 4 Chapter 2 Mind Map Mathematics Form 4 Chapter 2 Momentum Mathematics Form 4 Chapter 2 Notes Pdf Mathematics Form 4 Chapter 2 Objective Questions and Answers Mathematics Form 4 Chapter 2 Paper 2 Mathematics Form 4 Chapter 2 Slideshare Mathematics Form 4 Chapter 3 Mathematics Form 4 Chapter 3 Questions and Answers Mathematics Form 4 Chapter 4 Mathematics Form 4 Chapter 4 Notes Pdf Mathematics Form 4 Chapter 5 Light Questions and Answers Mathematics Form 4 Chapter 5 Notes Pdf Mathematics Form 4 Diagrams Mathematics Form 4 Exam Paper 1 Mathematics Form 4 Exams Mathematics Form 4 Exercise Mathematics Form 4 Exercise Pdf Mathematics Form 4 Module With Answer Mathematics Form 4 Note Mathematics Form 4 Notes Mathematics Form 4 Notes (Pdf) Mathematics Form 4 Notes All Chapter Pdf Mathematics Form 4 Notes and Questions Mathematics Form 4 Notes Chapter 1 Mathematics Form 4 Notes Chapter 2 Mathematics Form 4 Notes Chapter 3 Mathematics Form 4 Notes Download Mathematics Form 4 Notes Free Download Mathematics Form 4 Notes GCSE Mathematics Form 4 Notes KCSE-kcse Mathematics Form 4 Notes Pdf Mathematics Form 4 Notes Pdf Download Mathematics Form 4 Paper 2 Questions and Answers Mathematics Form 4 Past Papers Mathematics Form 4 Question Papers Mathematics Form 4 Questions Mathematics Form 4 Questions and Answers Mathematics Form 4 Questions and Answers Pdf Mathematics Form 4 Quiz Mathematics Form 4 Revision Notes Mathematics Form 4 Schemes of Work Mathematics Form 4 Summary Notes Mathematics Form 4 Syllabus Mathematics Form 4 Textbook Pdf Mathematics Form 4 Work Mathematics Form 5 Chapter 1 Exercise and Answers Mathematics Form 5 Chapter 1 Notes Pdf Mathematics Form 5 Chapter 2 Notes Pdf Mathematics Form 5 Chapter 2 Slideshare Mathematics Form 5 Chapter 3 Notes Pdf Mathematics Form 5 Notes Pdf Mathematics Form Four Book Mathematics Form Four Notes Mathematics Form Four Notes and Questions Mathematics Form Four Notes GCSE Mathematics Form Four Notes Pdf Mathematics Form Four Past Papers Mathematics Form Four Questions Mathematics Form Four Questions and Answers Mathematics Form Four Questions and Answers Pdf Mathematics Form Four Quiz Mathematics Form Four Study Notes Mathematics Form Four Syllabus Mathematics Form Four Topic 2 Mathematics Form Four Topic 4 Mathematics Form Four Topics Mathematics Form Four Work Mathematics Form One Mathematics Form One Book Mathematics Form One Book Pdf Mathematics Form One Download Topic 1 Upto 3 Mathematics Form One Exam Mathematics Form One Notes Mathematics Form One Notes and Questions Mathematics Form One Notes GCSE Mathematics Form One Notes Pdf Mathematics Form One Pdf Mathematics Form One Questions Mathematics Form One Questions and Answers Mathematics Form One Questions and Answers Pdf Mathematics Form One Questions and Their Answers Mathematics Form One Quiz Mathematics Form One Revision Question Mathematics Form One Schemes of Work Mathematics Form One Study Notes Mathematics Form One Syllabus Mathematics Form One Term Three Test Mathematics Form One to Three Notes Mathematics Form One Work Mathematics Form Three Mathematics Form Three Book Mathematics Form Three Notes Mathematics Form Three Notes and Questions Mathematics Form Three Notes GCSE Mathematics Form Three Questions and Answers Mathematics Form Three Questions and Answers Pdf Mathematics Form Three Quiz Mathematics Form Three Reproduction Mathematics Form Three Reproduction. Mathematics Form Three Study Notes Mathematics Form Three Work Mathematics Form Three-questions and Answers Mathematics Form Two Mathematics Form Two Book Mathematics Form Two Diagrams Mathematics Form Two Notes Mathematics Form Two Notes and Questions Mathematics Form Two Notes GCSE Mathematics Form Two Notes Pdf Mathematics Form Two Notes-pdf Mathematics Form Two Pdf Mathematics Form Two Questions Mathematics Form Two Questions and Answers Mathematics Form Two Questions and Answers Pdf Mathematics Form Two Quiz Mathematics Form Two Study Notes Mathematics Form Two Topics Mathematics Form Two Work Mathematics Form Two,schemes of Work Mathematics Form2 Mathematics Form2 Textbook Mathematics Game Form Four Question End Answers Mathematics Grade 10 Exam Papers Mathematics Hsc Pdf Mathematics Human Reproduction Video Mathematics IGCSE Past Papers Xtremepapers Mathematics K.c.s.e 2017 Mathematics KCSE Mathematics KCSE 2016 Mathematics KCSE 2017 Mathematics KCSE 2017 Paper 1 Mathematics KCSE Past Papers Mathematics KCSE Questions Mathematics KCSE Questions and Answer Mathematics KCSE Quizzes & Answers Mathematics KCSE Revision Mathematics KCSE Revision Notes Mathematics KCSE Setting Questions Form One and Two Mathematics Ksce 2015 Mathematics Last Year K.c.s.e Questions Mathematics Lesson Plan Form Two Mathematics Made Familiar Mathematics Mcq for Class 11 Mathematics Mcq for Class 12 Mathematics Mcq for Competitive Exams Mathematics Mcq for Competitive Exams Pdf Mathematics Mcq for Neet Pdf Mathematics Mcq for Ssc Mathematics Mcq Questions With Answers Mathematics Mcq With Answers Pdf Mathematics Mcqs for Class 12 Pdf Mathematics Mcqs With Answers Pdf Mathematics Mid Familia Form One Mathematics Mock Papers Mathematics Module Form 5 Mathematics Multiple Choice Questions and Answers Cxc Mathematics Multiple Choice Questions and Answers Pdf Mathematics Multiple Choice Questions With Answers Pdf Mathematics Note Mathematics Note Form Two All Chapters Mathematics Notes Mathematics Notes and Guestion and Answear Mathematics Notes and Syllabus Mathematics Notes Class 10 Mathematics Notes for Class 11 Pdf Mathematics Notes for Class 12 Pdf Mathematics Notes for High School Students Mathematics Notes for IGCSE 2014 Mathematics Notes Form 1 Mathematics Notes Form 1 4 Mathematics Notes Form 1 Free Download Mathematics Notes Form 1 KLB Mathematics Notes Form 1 Pdf Mathematics Notes Form 1-4 Mathematics Notes Form 1-4(1) Mathematics Mathematics Notes Form 14 Mathematics Notes Form 2 Mathematics Notes Form 2 KLB Mathematics Notes Form 2 Pdf Mathematics Notes Form 2; Mathematics Notes Mathematics Notes Form 3 Mathematics Notes Form 3 KLB Mathematics Notes Form 3 Pdf Mathematics Notes Form 4 Mathematics Notes Form 4 Chapter 2 Mathematics Notes Form 4 KLB Mathematics Notes Form 4 Pdf Mathematics Notes Form 4-pdf Mathematics Notes Form Four Mathematics Notes Form Four KLB Mathematics Notes Form Four Pdf Mathematics Notes Form One Mathematics Notes Form One KLB Mathematics Notes Form One Pdf Mathematics Notes Form One to Form Four Mathematics Notes Form Three Mathematics Notes Form Three KLB Mathematics Notes Form Three Pdf Mathematics Notes Form Two Mathematics Notes Form Two KLB Mathematics Notes Form Two Pdf Mathematics Notes Form2 Mathematics Notes IGCSE Mathematics Notes Kenya Mathematics Notes on Agroforestry Mathematics Notes Pdf Mathematics Notes: Mathematics Objective Answer Mathematics Objective Answer 2018 Mathematics Objective Questions for Competitive Exams Mathematics Objective Questions for Competitive Exams Pdf Mathematics Oral Exam Questions Mathematics Paper 1 Mathematics Paper 1 2018 Marking Rules Mathematics Paper 1 Notes Mathematics Paper 1 Questions Mathematics Paper 1 Questions and Answers Mathematics Paper 1 Topics Mathematics Paper 1 With Answers Mathematics Paper 2 Mathematics Paper 2 2017 Mathematics Paper 2 2018 Marking Rules Mathematics Paper 2 Questions and Answers Mathematics Paper 2 Questions and Answers Pdf Mathematics Paper 2 Revision Mathematics Paper 2 Topics Mathematics Paper 2018 Mathematics Paper 3 2018 Marking Rules Mathematics Paper 3 Question and Answer Mathematics Paper 3 Question Paper 2014 KCSE Mathematics Paper 3 Question Paper 2015 KCSE Mathematics Paper 3 Question Paper 2016 KCSE Mathematics Paper 3 Question Paper 2017 KCSE Mathematics Paper 3 Question Paper 2018 KCSE Mathematics Paper 3 Questions and Answers Mathematics Paper One Questions and Answers Mathematics Paper One Topics Mathematics Paper Two Qestions With Answers Mathematics Paper1 Mathematics Paper2 Mathematics Paper3 Mathematics Paper4 Mathematics Past Papers Mathematics Past Papers 2017 Mathematics Past Papers a Level Mathematics Past Papers Form 1 Mathematics Past Papers Form 2 Mathematics Past Papers Form 3 Mathematics Past Papers O Level Mathematics Pdf Download Mathematics Pp1 KCSE 2016 Mathematics Practical Book Class 12 Pdf Mathematics Practical Exam Mathematics Practicals Form One Mathematics Practicals Questions and Answers Mathematics Practice Test 9th Grade Mathematics Practice Test Answers Mathematics Practice Test Questions and Answers Mathematics Practice Test Quizlet Mathematics Predicted Questions This Year KCSE Mathematics Preparation Notes Mathematics Pretest High School Pdf Mathematics Question and Answer With Explanation Mathematics Question and Answers 2019 Mathematics Question and Answers 2021 Mathematics Question and Answers 2022 Mathematics Question and Answers 2023 Mathematics Question and Answers Note Mathematics Questions Mathematics Questions and Answers Mathematics Questions and Answers for High School Mathematics Questions and Answers for High Schools Mathematics Questions and Answers for High Schools Pdf Mathematics Questions and Answers for Secondary Schools Mathematics Questions and Answers Form 1 Mathematics Questions and Answers Form 2 Mathematics Questions and Answers Form 3 Mathematics Questions and Answers Form 4 Mathematics Questions and Answers Multiple Choice Mathematics Questions and Answers Notes Mathematics Questions and Answers O Mathematics Questions and Answers Online Mathematics Questions and Answers Pdf Mathematics Questions and Answers Pdf for Class 12 Mathematics Questions and Answers Pdf for Competitive Exams Mathematics Questions and Answers-form 2 Mathematics Questions for High School Mathematics Questions for High School Students With Answers Mathematics Questions for Senior 1 Mathematics Questions for Senior 2 Mathematics Questions for Senior 3 Mathematics Questions for Senior 4 Mathematics Questions for Senior 5 Mathematics Questions for Senior 6 Mathematics Questions for Senior Five Mathematics Questions for Senior Four Mathematics Questions for Senior One Mathematics Questions for Senior Six Mathematics Questions for Senior Three Mathematics Questions for Senior Two Mathematics Questions Form One Mathematics Questions Multiple Choice Mathematics Questions Quizlet Mathematics Questions to Ask Your Teacher Mathematics Quetion and Answer Form Four Mathematics Quetion and Answer Form One Mathematics Quetion and Answer Form Three Mathematics Quetion and Answer Form Two Mathematics Quiz for Class 9 Mathematics Quiz for Class 9 Mathematics Mathematics Quiz Questions and Answers for Class 10 Mathematics Quiz Questions and Answers for Class 10 Pdf Mathematics Quiz Questions and Answers for Class 12 Mathematics Quiz Questions and Answers for Class 9 Mathematics Quiz Questions and Answers for Class 9 Pdf Mathematics Quiz Questions and Answers for High School Mathematics Quiz Questions and Answers Multiple Choice Mathematics Quiz Questions and Answers Pdf Mathematics Quiz Questions for Class 12 Mathematics Quiz Questions for College Students Mathematics Quiz With Answers Mathematics Quiz With Answers Pdf Mathematics Quizlet Mathematics Revision Mathematics Revision a Level Mathematics Revision Mathematics Notes Mathematics Mathematics Revision Exam Mathematics Revision Examination Mathematics Revision Form One Mathematics Revision Notes Mathematics Revision Notes Mathematics Mathematics Revision Notes Form 1 Mathematics Revision Notes Form 2 Mathematics Revision Notes Form 3 Mathematics Revision Notes Form 4 Mathematics Revision Notes IGCSE Mathematics Revision Paper One Mathematics Revision Questions Mathematics Revision Questions and Answers Mathematics Revision Questions and Answers Form 1 Mathematics Revision Questions and Answers Form 2 Mathematics Revision Questions and Answers Form 3 Mathematics Revision Questions and Answers Form 4 Mathematics Revision Questions and Answers Form Four Mathematics Revision Questions and Answers Form One Mathematics Revision Questions and Answers Form Three Mathematics Revision Questions and Answers Form Two Mathematics Revision Questions Form 1 Mathematics Revision Questions Form 2 Mathematics Revision Questions Form 3 Mathematics Revision Questions Form 4 Mathematics Revision Questions Form Four Mathematics Revision Questions Form One Mathematics Revision Questions Form Three Mathematics Revision Questions Form Two Mathematics Revision Quiz Mathematics Revision Test Mathematics Secondary School Revision Mathematics Simple Notes Mathematics Spm Notes Download Mathematics Spm Notes Pdf Mathematics Spm Questions Mathematics Study Form 2 Mathematics Study Guide Mathematics Study Guide Answer Key Mathematics Study Guide Answers Mathematics Study Guide Mathematics Questions and Answers Mathematics Study Guide Ib Mathematics Study Guide Pdf Mathematics Study Guides Mathematics Study Notes Mathematics Study Notes Materials Form 1 Pdf Mathematics Study Notes Materials Form 2 3 Pdf Mathematics Study Notes Materials Form 2 Pdf Mathematics Study Notes Materials Form 3 Pdf Mathematics Study Notes Materials Form 4 Pdf Mathematics Syllabus in Kenya Mathematics Syllabus Pdf Mathematics Test 1 Quizlet Mathematics Test Questions Mathematics Test Questions and Answers Mathematics Test Questions and Answers Pdf Mathematics Topic One Form Four Mathematics Topics Form One Mathematics Unit 1 Quiz Mathematics Vol 3 Mathematics | Revision Mathematics Mathematics,form 4 Mathematics.form Four.topic Three MathematicsExam Form Three MathematicsModule Form 5 MathematicsNotes MathematicsNotes for Class 11 Pdf MathematicsNotes for Class 12 Pdf MathematicsNotes Form 1 MathematicsNotes Form 1 Free Download MathematicsNotes Form 2 MathematicsNotes Form 3 MathematicsNotes Form 3 Pdf MathematicsNotes IGCSE MathematicsNotes Pdf MathematicsPast Papers MathematicsQuestions and Answers Pdf MathematicsSimple Notes MathematicsSpm Notes Download MathematicsSpm Notes Pdf MathematicsSpm Questions MathematicsStudy Guide Answers MathematicsStudy Guide Pdf MathematicsStudy Guides Blologytextpapers Bridge Mathematics Business Past KCSE Past Papers Mathematics Form 3 Notes Pdf Mathematics Form 4 Notes Pdf C R E Form One KLB C R E Form One Oli Topic C.r.e Form 1 Notes Kenya C.r.e Form 2 Notes Kenya C.r.e Form 3 Notes C.r.e Form 3 Notes Kenya C.r.e Form 3 Pdf C.r.e Form 4 Notes Kenya C.r.e Form One Notes Pdf C.r.e Notes Form 1 C.r.e Revision Notes C.r.e Short Notes Cambridge IGCSE Mathematics Cambridge IGCSE Mathematics 3rd Edition Cambridge IGCSE Mathematics 3rd Edition Plus Cd South Asia Edition Cambridge IGCSE Mathematics Answers Cambridge IGCSE Mathematics Coursebook Pdf Download Cambridge IGCSE Mathematics Practical Workbook Cambridge IGCSE Mathematics Revision Guide Pdf Cambridge IGCSE Mathematics Study and Revision Guide 2nd Edition Pdf Cambridge IGCSE Mathematics Study and Revision Guide Pdf Cambridge IGCSE Mathematics Workbook Free Download Cambridge IGCSE Mathematics Workbook Pdf Cambridge IGCSE® Mathematics Coursebook Caucasian Chalk Circle Essay Questions Chapter 1 Introduction to Mathematics Chapter 1 Introduction to Mathematics Studies Cie a Level Mathematics Notes 2016 Cie a Level Mathematics Notes Pdf Cie Past Papers Class 10 Mathematics Chapter 1 Mcqs Class 8 Mathematics Notes KCSE-kcse College Mathematics Notes College Mathematics Practice Test College Mathematics Quiz College Mathematics Quiz Chapter 1 College Mathematics Quizlet College Mathematics Study Guide College Mathematics Study Guide Pdf College Mathematics Test Questions and Answers College Mathematics Volume 3 Pdf College MathematicsNotes Complete Mathematics for Cambridge IGCSE Complete Mathematics for Cambridge IGCSE Revision Guide Pdf County Mocks 2017 Cse Past Papers Mathematics 2017 Dl Mathematics Form 3 Pdf Kusoma Download Mathematics Form 1 Download Mathematics Form 2 Download Mathematics Form 2 Notes Download Mathematics Form 3 Download Mathematics Form 3 Notes Download Mathematics Form 4 Download Mathematics Form Four Download Mathematics Form One Download Mathematics Form Three Download Mathematics Form Two Download Mathematics Notes Form 3 Download Mathematics Notes Form One Download MathematicsNotes Form 3 Download Form Three Mathematics Notes Download Free KCSE Past Papers Mathematics Download Free KCSE Past Papers From KNEC. Download KCSE Past Papers With Answers Download KCSE Revision Notes Download KLB Mathematics Book 2 Download KLB Mathematics Book 3 Download KLB Mathematics Book 4 Download Notes of Mathematics Downloads | Mathematics | Form Four Exams | Exams Downloads | Mathematics | Form One Exams | Exams Downloads | Mathematics | Form Three Exams | Exams Downloads | Mathematics | Form Two Exams | Exams Downloads | KCSE Papers and Marking Schemes | Dvance KCSE Past Papers Easy Mathematics Questions Edexcel a Level Mathematics B Edexcel a Level Mathematics Notes Pdf Edexcel a Level Mathematics Salters Nuffield Edexcel A2 Mathematics Notes Edexcel as Mathematics Revision Guide Pdf Edexcel Mathematics A2 Revision Notes Pdf Edexcel Mathematics Unit 2 Revision Notes Edexcel GCSE Mathematics Revision Guide Pdf Edexcel IGCSE Mathematics Past Papers Edexcel IGCSE Mathematics Revision Guide Free Pdf Download Edexcel IGCSE Mathematics Revision Guide Pdf Edexcel IGCSE Mathematics Revision Guide Pdf Download Electronics Form Four Notes Energy Questions Mathematics Bowl Essay Questions and Answers KCSE Mathematics Notes Essay Questions and Answers on Betrayal in the City Essay Questions Based on Betrayal in the City Evolving World Mathematics Book 1 Pdf Evolving World Mathematics Book 4 Notes Evolving World Mathematics Book Form 1 Evolving World-history Book 3 Exam Notes for Mathematics 101 Exams KCSE Mathematics Paper 1 Questions and Answers F3 Mathematics Test Paper Find Download KCSE Past Papers With Answers Find KCSE Mathematics Essay Questions and Answers Form 1 Mathematics Exam Form 1 Mathematics Notes Form 1 Mathematics Questions and Answers Form 1 Mathematics Questions and Answers Pdf Form 1 Mathematics Revision Notes Form 1 Mathematics Summurized Revision Pdf Form 1 Mathematics Syllabus Form 1 Mathematics Test Paper Pdf Form 1 Mathematics Topics Form 1 MathematicsNotes Form 1 MathematicsQuestions and Answers Form 1 MathematicsRevision Notes Form 1 MathematicsSyllabus Form 1 MathematicsTest Paper Pdf Form 1 Past Papers Form 1 Past Papers With Answers Form 1 Revision Papers Form 1 Subjects in Kenya Form 2 Mathematics Exam Form 2 Mathematics Exam Paper Form 2 Mathematics Exam Paper 2016 Form 2 Mathematics Exam Paper Free Download Form 2 Mathematics Exam Paper With Answer Form 2 Mathematics Final Year Exam Paper 2 Form 2 Mathematics Notes Form 2 Mathematics Notes and Revision Questions Form 2 Mathematics Notes Pdf Form 2 Mathematics Past Papers Form 2 Mathematics Questions Form 2 Mathematics Questions and Answers Form 2 Mathematics Questions and Answers > Form 2 Mathematics Questions and Answers Pdf Form 2 Mathematics Revision Notes Form 2 Mathematics Short Notes Form 2 Mathematics Syllabus Form 2 MathematicsExam Paper Form 2 MathematicsExam Paper Free Download Form 2 MathematicsExam Paper With Answer Form 2 MathematicsFinal Year Exam Paper 2 Form 2 MathematicsPast Papers Form 2 MathematicsRevision Notes Form 2 MathematicsShort Notes Form 2 MathematicsSyllabus Form 2 Revision Papers Form 2 Subjects in Kenya Form 3 Mathematics Book Form 3 Mathematics Exam Form 3 Mathematics Exam Paper Form 3 Mathematics Notes Form 3 Mathematics Past Papers Form 3 Mathematics Questions Form 3 Mathematics Questions and Answers Form 3 Mathematics Questions and Answers Pdf Form 3 Mathematics Revision Notes Form 3 Mathematics Syllabus Form 3 MathematicsExam Paper Form 3 MathematicsNotes Form 3 MathematicsPast Papers Form 3 MathematicsQuestions Form 3 MathematicsQuestions and Answers Pdf Form 3 MathematicsRevision Notes Form 3 MathematicsSyllabus Form 3 C.r.e Form 3 Notes of Mathematics Topic on Fish Form 3 Past Papers Form 3 Revision Papers Form 3 Subjects in Kenya Form 4 Mathematics Exam Form 4 Mathematics Notes Form 4 Mathematics Notes Pdf Form 4 Mathematics Questions and Answers Form 4 Mathematics Questions and Answers Pdf Form 4 Mathematics Revision Notes Form 4 Mathematics Syllabus Form 4 Mathematics Topics Form 4 MathematicsNotes Form 4 MathematicsRevision Notes Form 4 MathematicsSyllabus Form 4 MathematicsTopics Form 4 Exam Papers Form 4 Revision Papers Form 4 Subjects in Kenya Form 5 Mathematics Topics Form 5 MathematicsTopics Form Five Mathematics Notes Form Five MathematicsNotes Form Four Mathematics Book Form Four Mathematics Notes Form Four Mathematics Notes Pdf Form Four Mathematics Questions and Answers Form Four Mathematics Questions and Answers Pdf Form Four Mathematics Revision Questions Form Four Mathematics Syllabus Form Four Mathematics Topics Form Four MathematicsNotes Form Four MathematicsQuestions and Answers Form Four MathematicsQuestions and Answers Pdf Form Four MathematicsTopics Form Four Notes Form Four Revision Papers Form Four Subjects in Kenya Form One Mathematics Book Form One Mathematics Examination Form One Mathematics First Topic Form One Mathematics Lesson Plan Form One Mathematics Notes Pdf Form One Mathematics Past Papers Pdf Form One Mathematics Questions Form One Mathematics Questions and Answers Form One Mathematics Questions and Answers Pdf Form One Mathematics Revision Questions Form One Mathematics Short Notes Form One Mathematics Syllabus Form One Mathematics Topics Form One MathematicsExamination Form One MathematicsPast Papers Pdf Form One MathematicsQuestions and Answers Form One MathematicsQuestions and Answers Pdf Form One MathematicsTopics Form One Exams Form One Notes of Mathematics Form One Past Papers Form One Subjects in Kenya Form One Term One Mathematics Exam Form One Term One MathematicsExam Form Three Mathematics Book Form Three Mathematics Book Pdf Form Three Mathematics Notes Form Three Mathematics Notes Pdf Form Three Mathematics Questions and Answers Form Three Mathematics Questions and Answers Pdf Form Three Mathematics Revision Questions Form Three Mathematics Syllabus Form Three Mathematics Topics Form Three MathematicsNotes Form Three MathematicsNotes Pdf Form Three MathematicsQuestions and Answers Form Three MathematicsQuestions and Answers Pdf Form Three MathematicsTopics Form Three Subjects in Kenya Form Two Mathematics Book Form Two Mathematics Cat Form Two Mathematics Examination Form Two Mathematics Notes Form Two Mathematics Notes Pdf Form Two Mathematics Past Papers Form Two Mathematics Questions and Answers Form Two Mathematics Questions and Answers Pdf Form Two Mathematics Revision Questions Form Two Mathematics Syllabus Form Two Mathematics Topics Form Two MathematicsNotes Form Two MathematicsNotes Pdf Form Two MathematicsQuestions and Answers Form Two MathematicsQuestions and Answers Pdf Form Two MathematicsSyllabus Form Two MathematicsTopics Form Two Notes Form Two Subjects in Kenya Free a-level Mathematics Revision App | Pass Your Mathematics Exams Free Mathematics Form 1 Notes Free Mathematics Notes Form 1 Free Mathematics Notes Pdf Free MathematicsNotes Pdf Free College Mathematics Practice Test Free Form1,form2,form3 Past Papers Free KCSE Past Papers Free KCSE Mocks 2015 Free KCSE Past Papers 2014 Free KCSE Past Papers KCSE Past Free KCSE Past Papers Kenya, Free KCSE Past Papers With Answers Free KCSE Questions and Answers on Mathematics Free KCSE Revision Notes Free Marking Schemes Free Mocks Online KCSE Answers Past Exams Question Papers Free Revision Papers From Three Notes Topic One KLB Fun Mathematics Questions Funny Mathematics Questions Funny Mathematics Questions and Answers Funny Mathematics Questions to Ask Funny Mathematics Quotes GCSE Mathematics Exam Questions and Answers GCSE Mathematics Past Papers GCSE Mathematics Revision GCSE Mathematics Revision Notes GCSE Mathematics Revision Notes Pdf GCSE Mathematics Revision Notes Pdf 9-1 GCSE Mathematics Revision Questions and Answers GCSE Mathematics Textbook Pdf GCSE Mathematics Topics Pass My Exams: Easy Exam Revision Notes Home Mathematics Notes Pdf Home Mathematics Practice Test With Answers Home Mathematics Quiz Home Mathematics Quiz Pdf Home Mathematics Test Questions and Answers Home Mathematics Test Questions and Answers Pdf Home Knowledge in Mathematics Human Body Good Mathematics Questions to Ask GRE Mathematics Practice Test GRE Mathematics Subject Test Pdf Handbook of Mathematics Pdf Free Download Hard Mathematics Questions Hard Mathematics Questions and Answers Hard Mathematics Questions to Ask Your Teacher Hard Mathematics Quiz Questions Hard Form 3 Mathematics Question High School Mathematics Final Exam Doc High School Mathematics Final Exam Pdf High School Mathematics Final Exam Questions High School Mathematics Final Exam Questions and Answers High School Mathematics Notes High School Mathematics Practice Test High School Mathematics Pretest With Answers High School Mathematics Questions and Answers Pdf High School Mathematics Study Guide High School Mathematics Test Questions and Answers Pdf High School MathematicsNotes High School MathematicsStudy Guide How to Answer KCSE Mathematics Question How to Motivate a Form 4 Student How to Motivate a KCSE Candidate How to Motivate a KCSE Student How to Pass Mathematics Questions & Answers Form 1&2 | Text Book How to Revise Mathematics How to Revise Effectively for KCSE How to Study Mathematics: 5 Study Techniques to Master Mathematics Hsc Mathematics 2018 Hsc Mathematics 2019 Https://www.knec.ac.ke/ Www.knec-portal.ac.ke/ KNEC Portal: Ial Mathematics Notes Ib Mathematics Cold War Notes Ib Mathematics Notes Ib Mathematics Notes Pdf Ib Mathematics of the Americas Notes Ib Mathematics of the Americas Study Guide Ib Mathematics Paper 2 Study Guide Ib Mathematics Question Bank by Topic Ib Mathematics Study Guide Pdf Ict Notes Form 1 IGCSE Mathematics Alternative to Practical Revision IGCSE Mathematics Alternative to Practical Revision Notes IGCSE Mathematics Book IGCSE Mathematics Book Pdf Download IGCSE Mathematics Notes IGCSE Mathematics Notes 2017 Pdf IGCSE Mathematics Notes Edexcel IGCSE Mathematics Paper 2 Notes IGCSE Mathematics Paper 6 Notes IGCSE Mathematics Past Papers IGCSE Mathematics Past Papers 2014 IGCSE Mathematics Past Papers 2017 IGCSE Mathematics Pdf IGCSE Mathematics Pre Release Material 2018 IGCSE Mathematics Resources IGCSE Mathematics Revision Guide IGCSE Mathematics Revision Guide Free Download IGCSE Mathematics Revision Guide Pdf Download IGCSE Mathematics Revision Notes Pdf IGCSE Mathematics Revision Worksheets IGCSE Mathematics Workbook Pdf IGCSE Mathematics Znotes IGCSE MathematicsPast Papers IGCSE Notes Mathematics Importance of Agroforestry Inorganic Mathematics Multiple Choice Questions With Answers Pdf Inorganic Mathematics Questions and Answers Pdf Interesting Mathematics Questions Interesting Mathematics Questions and Answers Interesting Questions to Ask About Mathematics Intro to Mathematics Quiz Introduction of Mathematics Form One Introduction to Mathematics Introduction to Mathematics Notes Introduction to Mathematics Pdf Introduction to MathematicsNotes Is Agroforestry Sustainable? K.c.s.e Answers Mathematics Paper One 2018 K.c.s.e Mathematics 2017 K.c.s.e Mathematics 2018 K.c.s.e Mathematics Paper 1 2017 K.c.s.e Mocks 2018 K.c.s.e Papers 2015 K.c.s.e Papers 2016 K.c.s.e Past Papers 2014 K.c.s.e.Mathematics Paper 2 Year 2018 K.c.s.e.results 2018 for Busia County K.l.b Mathematics Form 3 K.l.b Mathematics Notes K.l.b MathematicsNotes Kasneb Past Papers for Colleges Mathematics Past Papers KCSE 2010 Marking Scheme KCSE 2010 Past Papers KCSE 2011 Mathematics Paper 1 KCSE 2011 Marking Scheme KCSE 2012 Mathematics Paper 2 Marking Scheme KCSE 2012 Marking Schemes KCSE 2013 Mathematics Paper 1 KCSE 2013 Marking Scheme KCSE 2013 Marking Scheme Pdf KCSE 2014 KCSE 2015 Mathematics Paper 2 KCSE 2015 Mathematics Paper 3 KCSE 2015 Marking Scheme KCSE 2015 Past Papers KCSE 2016 Mathematics Paper 1 KCSE 2016 Mathematics Paper 2 KCSE 2017 Mathematics Paper 1 KCSE 2017 Mathematics Paper 2 KCSE 2017 Hostory Papers With Answers.com KCSE 2017 Marking Scheme KCSE 2017 Papers KCSE 2017 Papers and Marking Scheme KCSE 2017 Papers Pdf KCSE 2017 Past Papers KCSE 2017 Prediction Pdf KCSE 2018 Mathematics and Answers KCSE 2018 Mathematics Prediction KCSE 2018 Leakage KCSE 2018 Marking Scheme KCSE 2018 Papers KCSE 2018 Prediction Pdf KCSE 2018 Predictions KCSE 2018 Questions KCSE 2018 Questions and Answers KCSE 2019 Leakage Mathematics KCSE 2019 Marking Scheme KCSE 2019 Questions KCSE 2019 Questions and Answers KCSE 2021 Questions KCSE 2021 Questions and Answers KCSE Answers KCSE Answers Past Exams Question Papers Downloads | KCSE Mathematics 2011 KCSE Mathematics 2016 KCSE Mathematics Diagramsbiology Revision Tips KCSE Mathematics Essay Questions and Answers KCSE Mathematics Essay Questions and Answers Pdf KCSE Mathematics Essays KCSE Mathematics Essays Pdf KCSE Mathematics Marking Schemes KCSE Mathematics Notes KCSE Mathematics Notes Pdf KCSE Mathematics Notes, Syllabus, Questions, Answers KCSE Mathematics Paper 1 KCSE Mathematics Paper 1 2011 KCSE Mathematics Paper 1 2012 KCSE Mathematics Paper 1 2013 KCSE Mathematics Paper 1 2015 KCSE Mathematics Paper 1 2016 KCSE Mathematics Paper 1 2017 KCSE Mathematics Paper 1 2017 Pdf KCSE Mathematics Paper 1 Questions and Answers KCSE Mathematics Paper 2 KCSE Mathematics Paper 2 2012 KCSE Mathematics Paper 2 2012 KCSE Mathematics Paper 2 2015 KCSE Mathematics Paper 2 2013 KCSE Mathematics Paper 2 2014 KCSE Mathematics Paper 2 2015 KCSE Mathematics Paper 2 2016 KCSE Mathematics Paper 2 2017 KCSE Mathematics Paper 3 KCSE Mathematics Paper 3 2012 KCSE Mathematics Paper 3 2016 KCSE Mathematics Paper 3 2017 KCSE Mathematics Paper 3 Past Papers KCSE Mathematics Past Papers KCSE Mathematics Past Papers and Answers KCSE Mathematics Past Papers Pdf KCSE Mathematics Practical KCSE Mathematics Practical 2015 KCSE Mathematics Practical 2016 KCSE Mathematics Practical Past Papers KCSE Mathematics Practicals KCSE Mathematics Practicals KCSE Mathematics Paper 1 KCSE Mathematics Question and Answer KCSE Mathematics Questions and Answers KCSE Mathematics Questions and Answers Ap Mathematics KCSE Mathematics Revision KCSE Mathematics Revision Notes KCSE Mathematics Revision Papers KCSE Mathematics Revision Questions KCSE Mathematics Revision Questions and Answers KCSE Mathematics Syllabus KCSE MathematicsNotes KCSE MathematicsPaper 1 KCSE MathematicsPaper 2 KCSE MathematicsPaper 2 Pdf KCSE MathematicsSyllabus KCSE Business Paper 1 2016 KCSE Business Past Papers KCSE Mathematics Past Papers KCSE Essay Questions in Betrayal in the City KCSE Essays KCSE Exam Papers 2018 KCSE Exam Papers Answers KCSE Form 1 Mathematics Revision KCSE Form 2 Mathematics Revision KCSE Form 3 Mathematics Revision KCSE Form 4 Mathematics Revision KCSE Form Four Mathematics Revision KCSE Form One Mathematics Revision KCSE Form Three Mathematics Revision KCSE Form Two Mathematics Revision KCSE KCSE Past Papers KNEC KCSE Leakage KCSE Leakage Mathematics KCSE Made Familiar Mathematics KCSE Made Familiar Mathematics Pdf KCSE Marking Scheme 2016 KCSE Marking Schemes KCSE Marking Schemes 2017 KCSE Marking Schemes Pdf KCSE Mock Exams KCSE Mock Papers 2015 KCSE Mock Papers 2017 KCSE Mock Papers 2018 KCSE Mock Papers Pdf KCSE Mock Papers Pdf 2018 KCSE Mock Papers Pdf KCSE Past Papers KCSE Mocks 2017 KCSE Mocks 2018 KCSE Notes KCSE Online Notes KCSE Online Past Papers KCSE Online Registration KCSE Papers 2015 KCSE Papers and Marking Schemes | Exams KCSE Past Papers KCSE Past Papers 2007 KCSE Past Papers 2009 KCSE Past Papers 2010 KCSE Past Papers 2011 KCSE Past Papers 2011 Pdf KCSE Past Papers 2012 KCSE Past Papers 2013 KCSE Past Papers 2013knec KCSE Past Papers 2014 KCSE Past Papers 2014 Pdf KCSE Past Papers 2015 KCSE Past Papers 2015 Marking Schemes KCSE Past Papers 2015 Pdf KCSE Past Papers 2016 KCSE Past Papers 2016 Pdf KCSE Past Papers 2017 KCSE Past Papers 2017 Pdf KCSE Past Papers 2018 KCSE Past Papers Mathematics KCSE Past Papers Mathematics and Answers KCSE Past Papers Mathematics Pdf KCSE Past Papers Mathematics With Answers KCSE Past Papers Mathematicsand Answers KCSE Past Papers Mathematics and Answers KCSE Past Papers KCSE and Answers KCSE Past Papers KCSE and Answers Free Mocks Online KCSE Past Papers Marking Scheme KCSE Past Papers Pdf Download KCSE Past Papers Pdf Download KCSE 2013 KCSE Past Papers With Answers KCSE Past Papers Woodwork and Answers KCSE Prediction 2017 KCSE Prediction 2018 KCSE Prediction 2018 Pdf KCSE Prediction Papers 2018 KCSE Prediction Questions KCSE Prediction Questions 2018 KCSE Prediction Questions and Answers KCSE Questions KCSE Questions and Answers KCSE Questions and Answers. KCSE Questions on Mathematics KCSE Results, Online Registration, KCSE Result Slip. KCSE Revision KCSE Revision Notes KCSE Revision Notes Mathematics KCSE Revision Notes Pdf KCSE Revision Papers KCSE Revision Papers 2014 KCSE Revision Papers With Answers KCSE Revision Question for Mathematics KCSE Revision Questions KCSE Revision Questions and Answers KCSE Revision | Secondary School | Text Books | Text Book Centre KCSE Syllabus Pdf KCSE Trial 2017 KCSE Trial Exams 2017 Kenya Secondary School Mathematics Syllabus Kenya Secondary School Mathematics Syllabus Pdf Kenya Secondary School MathematicsSyllabus Pdf Kenya Secondary School Syllabus Pdf Kenya-kcse-christian Religious Education Syllabus Kenyaplex KCSE Past Papers Kenyaplex Past Papers for Secondary KLB Mathematics Book 1 Download KLB Mathematics Book 1 Notes KLB Mathematics Book 1 Pdf KLB Mathematics Book 2 KLB Mathematics Book 2 Notes KLB Mathematics Book 2 Notes Pdf KLB Mathematics Book 2 Pdf KLB Mathematics Book 3 Notes KLB Mathematics Book 3 Pdf KLB Mathematics Book 3 Pdf Download KLB Mathematics Book 4 Notes KLB Mathematics Book 4 Pdf KLB Mathematics Book 4 Pdf Download KLB Mathematics Book 4 Topics KLB Mathematics Book One KLB Mathematics Form 1 KLB Mathematics Form 1 Notes KLB Mathematics Form 1 Pdf KLB Mathematics Form 2 KLB Mathematics Form 2 Book KLB Mathematics Form 2 Notes KLB Mathematics Form 2 Pdf KLB Mathematics Form 2 Pdf Download KLB Mathematics Form 2 Schemes of Work KLB Mathematics Form 3 KLB Mathematics Form 3 Notes KLB Mathematics Form 3 Notes Pdf KLB Mathematics Form 3 Pdf KLB Mathematics Form 3 Pdf Download KLB Mathematics Form 4 KLB Mathematics Form 4 Notes KLB Mathematics Form 4 Pdf KLB Mathematics Form Four KLB Mathematics Form Four Notes KLB Mathematics Form One KLB Mathematics Form One Notes KLB Mathematics Form Three KLB Mathematics Form Three Notes KLB Mathematics Form Two KLB Mathematics Form Two Notes KLB Mathematics Notes KLB Mathematics Notes Form 4 KLB Mathematics Pdf KLB MathematicsNotes KLB MathematicsNotes Form 4 KLB MathematicsPdf KNEC Mathematics Syllabus KNEC Examiners Portal KNEC Website KNEC Ict Past Papers KNEC Past Papers for Colleges KNEC Past Papers Free Download KNEC Past Papers Free Downloads KNEC Past Papers Pdf KNEC Portal Confirmation KNEC Portal KCSE Results KNEC Portal KNEC Past Papers for Colleges Kasneb Past Papers KNEC Revision Papers KNEC Technical Exams Past Papers Kusoma Mathematics Notes Kusoma Mathematics Notes Pdf Kusoma Notes Mathematics Kusoma.co.ke Kusoma.com Past Papers Learner Guide for Cambridge IGCSE Mathematics Longhorn Mathematics Book 3 Pdf Made Familiar Mathematics Made Familiar Mathematics Pdf Made Familiar Mathematics Questions Maktaba Tetea Notes Marking Scheme KCSE Mathematics Past Papers Math Form2 Note Mcqs About Gaseous Exchange Middle School Mathematics Bowl Mathematics Questions Mock Past Papers 2017 Mock Past Papers With Answers Mokasa Mock 2017 More Than 1800 Mathematics Questions and Answers to Help You Study Multiple Choice Questions on Mathematics Necta Mathematics Past Papers Necta Mathematics Practicals Necta MathematicsPast Papers Necta MathematicsPracticals Necta Form Four Past Papers Necta Past Papers Form 4 Necta Past Papers Form 4 2016 Necta Past Papers Form Six Necta Past Papers Form Two Necta Questions and Answers Necta Review Questions Notes Mathematics Form 1 Notes Mathematics Form 2 Notes Mathematics Form 3 Notes Mathematics Form 3 Notes Pdf Notes Mathematics Form 3 Syllabus Notes Mathematics Form 4 Syllabus Notes on Mathematics Studies Notes Za Mathematics 4m 2 Notes Za Mathematics Form One Notes Za Mathematics Form Three O Level Mathematics Practical Experiments O Level Mathematics Questions and Answers Pdf Orm Three Mathematics Notes Page Navigation Papacambridge Mathematics IGCSE Papers KNEC KCSE Online Past Papers KNEC KCSE Results Past Papers Past KCSE Papers Past Paper Questions by Topic Mathematics Past Papers 2014 Past Papers in Kenya Pdf Mathematics Form 3 Pdf Mathematics Notes Pdf Mathematics Notes Form 1 Pdf Mathematics Notes Form 2 Pdf Mathematics Notes Form 3 Pdf Mathematics Notes Form 4 Pdf Mathematics Notes Form Four Pdf Mathematics Notes Form One Pdf Mathematics Notes Form Three Pdf Mathematics Notes Form Two Pdf Form 1 Mathematics Questions and Answers Pdf Form 2 Mathematics Questions and Answers Pdf Form 3 Mathematics Questions and Answers Pdf Form 4 Mathematics Questions and Answers Pdf Form Four Mathematics Questions and Answers Pdf Form One Mathematics Questions and Answers Pdf Form Three Mathematics Questions and Answers Pdf Form Two Mathematics Questions and Answers Pdf Free KCSE Past Papers and Marking Schemes Pdf" Revision Questions Mathematics Form 1 Practical Mathematics Experiments Pdf Practical Mathematics Question and Answer Pdf Pre Mocks 2018 Preliminary Mathematics Primary and Secondary Tillage Implements Ppt Pte KNEC Past Papers Questions and Answers Pdf Mathematics Form 1 Questions and Answers Pdf Mathematics Form 2 Questions and Answers Pdf Mathematics Form 3 Questions and Answers Pdf Mathematics Form 4 Questions and Answers Pdf Mathematics Form Four Questions and Answers Pdf Mathematics Form One Questions and Answers Pdf Mathematics Form Three Questions and Answers Pdf Mathematics Form Two Questions Based to Introduction to Mathematics Questions on Gaseous Exchange in Humans Questions on Introduction to Mathematics Questions to Ask in Mathematics Class Questions to Confuse Your Mathematics Teacher Quizlet Mathematics Test Quizlet Test Questions Qustions in Mathematics and Answers Revision Revision Mathematics Notes and Questions? Revision Quiz for Mathematics for Form Three S.1 Mathematics Questions S.2 Mathematics Questions S.3 Mathematics Questions S.4 Mathematics Questions Sample Essays on Betrayal in the City School Mathematics Notes Secondary Mathematics Notes Secondary Mathematics Notes Pdf Secondary MathematicsNotes Pdf Senior 1 Mathematics Notes Senior 2 Mathematics Notes Senior 3 Mathematics Notes Senior 4 Mathematics Notes Senior 5 Mathematics Notes Senior 6 Mathematics Notes Senior Five Mathematics Notes Senior Four Mathematics Notes Senior One Mathematics Notes Senior Six Mathematics Notes Senior Three Mathematics Notes Senior Two Mathematics Notes Simple Scientific Questions Smart Questions to Ask a Mathematics Teacher Snab Mathematics Revision Notes Southwest Mock Paper 2 2016 Mathematics Only Spm Mathematics Revision Notes Spm Notes Success Mathematics Spm Pdf Success MathematicsSpm Pdf Summary of Mathematics Form 3 Tahossa Past Papers To Motivate a Form 4 KCSE Student To Motivate a Form 4 Student Topical Revision Material Tricky Mathematics Questions and Answers Tricky Mathematics Questions for Adults Tricky Mathematics Questions With Answers Tricky Mathematics Quiz Questions Two Mathematics Revision Questions University Mathematics Volume 3 Openstax University Mathematics Volume 3 Pdf University Mathematics Volume 4 Pdf Ur Revision Guide IGCSE Mathematics What Are the Types of Gametes Working of Excretory System Www.Mathematics Form One Notes.com Www.Mathematics From One KLB.com Www.form 1 Mathematics.com Www.form 2 Mathematics.com Www.form 3 Mathematics.com Www.form 4 Mathematics.com Www.form Four Mathematics.com Www.form One Mathematics.com Www.form Three Mathematics.com Www.form Two Mathematics.com Www.kusoma Notes Www.kusoma Revision Materials Www.kusoma.co.ke Mathematics Notes Xtremepapers IGCSE Mathematics Year 11 Mathematics Z Notes Mathematics IGCSE Znotes as Mathematics "Pdf" Revision Questions Maths Form 1 "Pdf" Revision Questions Maths Form 2 "Pdf" Revision Questions Maths Form 3 "Pdf" Revision Questions Maths Form 4 "Pdf" Revision Questions Maths Form Four "Pdf" Revision Questions Maths Form One "Pdf" Revision Questions Maths Form Three "Pdf" Revision Questions Maths Form Two 1 a a KCSE Past Papers 10th Grade Maths Questions and Answers 10th Grade Maths Test 11th Ncert Maths 12th Class Maths Book Free Download 2014 KCSE Marking Schemes 2014 Pdf KCSE Past Papers 2015 2015 Maths Essay Questions and Answers Form 4 2016 KCSE Papers 2016 KCSE Prediction Questions 2017 Maths Hsc Answers 2017 KCSE Prediction Questions 2018 Maths KCSE Leakage 2018 Maths KCSE Questions 2018 KCSE Busineness Studies 2018 KCSE Exam 2018 KCSE Leakage 2018 KCSE Prediction Questions 2018 KCSE Questions 2019 Maths KCSE Leakage 2019 Maths KCSE Questions 2019 KCSE Leakage 2019 KCSE Questions 9th Grade Maths Study Guide A a a Maths Notes a a a Maths Notes! a a a MathsNotes! A a KCSE Past Papers A Biblical View of Social Justice A Level Maths Biological Molecules Questions A Level Maths Exam Questions by Topic A Level Maths Notes Edexcel A Level Maths Notes Xtremepapers A Level Maths Past Papers A Level Maths Questions and Answers a Level Maths Questions and Answers A Level Maths Questions and Answers (Pdf) A Level Maths Questions and Answers Pdf A Level Maths Questions by Topic Kidney Questions With Markschemes A Level Maths Revision A Level Maths Revision Edexcel A Level Maths Revision Guide A Level Maths Revision Notes A Level Maths Revision Notes Pdf A Level Maths Textbook Pdf A Level Maths Year 1 / as Aqa Exam Questions by Topic A Level Edexcel Notes a* Maths aa Maths Form 3 Questions and Answers Advance KCSE Past Papers Advance-africa.com KCSE Rev Quiz Advantages and Disadvantages. All Maths Essays All Maths Notes for Senior Two All KCSE Past Papers Maths With Making Schemes All Marking Schemes Questions and Answers All Past K.c.s.e Questions With Answers Alliance Mocks 2017 Ap Bio Quizzes Ap Maths 1 Textbook Pdf Ap Maths Essay Questions and Answers Are Sourced From KNEC. As Level Maths Notes Atika Maths Notes Atika School Maths Notes B/s Book 2 Notes Basic Maths Books Pdf basic Maths Interview Questions and Answers Pdf Basic Maths Interview Questions and Answers Pdf Basic Maths Pdf Basic Maths Questions and Answers Basic Maths Questions and Answers Pdf Bbc Bitesize Maths Ks3 Bihar Board Maths Objective Answer 2017 Bihar Board Maths Objective Answer 2018 Bio Answers Bio Quesions Maths 0478 Maths 101 Maths 12th Maths 12th Class Notes Pdf Maths 2019 Syllabus Maths All KCSE Short Notes Maths Answers Maths Answers Online Free Maths Answers Quizlet Maths Bk 2 Notes Maths Book 1 Maths Book 1 Notes Maths Book 2 Maths Book 2 Notes Maths Book 3 Maths Book 3 KLB Maths Book 3 Notes Maths Book 4 Maths Book 4 Notes Maths Book 4 Pdf Maths Book for Class 11 Maths Book Four Maths Book Four Notes Maths Book One Maths Book One Notes Maths Book Pdf Free Download Maths Book Three Maths Book Three Notes Maths Book Three Pdf Maths Book Two Maths Book Two Notes Maths Books Form Three Maths Bowl Maths Study Guide Maths Bowl Questions Maths Maths Bowl Questions Earth Maths Maths Bowl Questions Math Maths Bowl Questions Middle School Maths Brekthrough Form Two Notes Maths Class 12 Ncert Solutions Maths Class 12 Pdf Maths Communication Syllabus Maths Diagram Software Maths Diagrams for Class 11 Maths Diagrams for Class 12 Maths Diagrams for Class 9 Maths Diagrams for Class-10 Maths Diagrams in Form 1 Maths Diagrams in Form 2 Maths Diagrams in Form 3 Maths Diagrams in Form 4 Maths Diagrams Pdf Maths Diagrams to Label Maths Essay Questions and Answers Maths Essay Questions and Answers 2018 Maths Essay Questions and Answers Form 1 Maths Essay Questions and Answers Form 2 Maths Essay Questions and Answers Form 3 Maths Essay Questions and Answers Form 4 Maths Essay Questions and Answers Form 4 Pdf Maths Essay Questions and Answers Pdf Maths Essay Revision Q Maths Essays and Answers Maths Essays Form One to Form Four Maths Essays Form One to Form Three Maths Essays KCSE Maths Essays Pdf Maths Exam 1 Multiple Choice Maths Exam 2 Advance Maths Exam 2 Test Maths Exam 2016 Maths Exam Form Four Maths Exam Form One Maths Exam Form Three Maths Exam Form Two Maths Exam Practice Test Maths Exam Questions Maths Exam Questions and Answers Maths Exam Questions and Answers Pdf Maths Exam Study Guide Maths Exams Maths Excretion Notes Maths Exercise Form 4 With Answers Maths Final Exam Answer Key Maths Final Exam Answer Key 2016 Maths Final Exam Answer Key 2017 Maths Final Exam Answers 2018 Maths Final Exam Answers 2019 Maths Final Exam Questions and Answers Maths Fom 1 Notes Maths Fom 2 Notes Maths Fom 3 Notes Maths Fom 4 Notes Maths Form 1 Maths Form 1 & 2 and Answers Maths Form 1 and 2 Essays Maths Form 1 and 2 Essays Questions and Answers Maths Form 1 Chapter 1 Maths Form 1 Diagrams Maths Form 1 Exams Maths Form 1 Mid Year Exam Maths Form 1 Notes Maths Form 1 Notes and Questions Maths Form 1 Notes Download Maths Form 1 Notes Free Download Maths Form 1 Notes GCSE Maths Form 1 Notes KCSE-kcse Maths Form 1 Notes Pdf Maths Form 1 Notes Pdf Download Maths Form 1 Past Papers Maths Form 1 Pdf Maths Form 1 Pressure Maths Form 1 Question Papers Maths Form 1 Questions Maths Form 1 Questions and Answers Maths Form 1 Questions and Answers Pdf Maths Form 1 Quiz Maths Form 1 Revision Questions Maths Form 1 Summary Notes Maths Form 1 Syllabus Maths Form 1 Work Maths Form 1-4 Notes Maths Form 2 Maths Form 2 Chapter 1 Maths Form 2 Chapter 2 Maths Form 2 Diagrams Maths Form 2 Exam Paper 2014 Maths Form 2 Exams Maths Form 2 Notes Maths Form 2 Notes and Questions Maths Form 2 Notes GCSE Maths Form 2 Notes KCSE-kcse Maths Form 2 Notes Pdf Maths Form 2 Notes Pdf Download Maths Form 2 Past Papers Maths Form 2 Pdf Maths Form 2 Question Papers Maths Form 2 Questions Maths Form 2 Questions and Answers Maths Form 2 Questions and Answers Pdf Maths Form 2 Quiz Maths Form 2 Revision Notes Maths Form 2 Salts Maths Form 2 Structure and Bonding Maths Form 2 Summary Notes Maths Form 2 Syllabus Maths Form 2 Work Maths Form 3 Maths Form 3 and 4 Essays Maths Form 3 and 4 Essays Questions and Answers Maths Form 3 Chapter 3 Maths Form 3 Classification Maths Form 3 Diagrams Maths Form 3 Ecology Maths Form 3 Exams Maths Form 3 Notes Maths Form 3 Notes and Questions Maths Form 3 Notes GCSE Maths Form 3 Notes KCSE-kcse Maths Form 3 Notes Pdf Maths Form 3 Notes Pdf Download Maths Form 3 Notes Topic 1 Maths Form 3 Past Papers Maths Form 3 Pdf Maths Form 3 Question Papers Maths Form 3 Questions Maths Form 3 Questions and Answers Maths Form 3 Questions and Answers Pdf Maths Form 3 Questions and Answers Term 3 Maths Form 3 Questions and Answers+pdf Maths Form 3 Quiz Maths Form 3 Revision Notes Maths Form 3 Revision Questions Maths Form 3 Summary Notes Maths Form 3 Syllabus Maths Form 3 Syllabus Pdf Maths Form 3 Topics Maths Form 3 Work Maths Form 4 Maths Form 4 All Chapter Maths Form 4 Chapter 1 Conversion of Units Maths Form 4 Chapter 1 Exercise Maths Form 4 Chapter 1 Exercise and Answers Maths Form 4 Chapter 1 Exercise Pdf Maths Form 4 Chapter 1 Mind Map Maths Form 4 Chapter 2 Maths Form 4 Chapter 2 Exercise and Answers Maths Form 4 Chapter 2 Exercise Pdf Maths Form 4 Chapter 2 Experiment Maths Form 4 Chapter 2 Formula Maths Form 4 Chapter 2 Mind Map Maths Form 4 Chapter 2 Momentum Maths Form 4 Chapter 2 Notes Pdf Maths Form 4 Chapter 2 Objective Questions and Answers Maths Form 4 Chapter 2 Paper 2 Maths Form 4 Chapter 2 Slideshare Maths Form 4 Chapter 3 Maths Form 4 Chapter 3 Questions and Answers Maths Form 4 Chapter 4 Maths Form 4 Chapter 4 Notes Pdf Maths Form 4 Chapter 5 Light Questions and Answers Maths Form 4 Chapter 5 Notes Pdf Maths Form 4 Diagrams Maths Form 4 Exam Paper 1 Maths Form 4 Exams Maths Form 4 Exercise Maths Form 4 Exercise Pdf Maths Form 4 Module With Answer Maths Form 4 Note Maths Form 4 Notes Maths Form 4 Notes (Pdf) Maths Form 4 Notes All Chapter Pdf Maths Form 4 Notes and Questions Maths Form 4 Notes Chapter 1 Maths Form 4 Notes Chapter 2 Maths Form 4 Notes Chapter 3 Maths Form 4 Notes Download Maths Form 4 Notes Free Download Maths Form 4 Notes GCSE Maths Form 4 Notes KCSE-kcse Maths Form 4 Notes Pdf Maths Form 4 Notes Pdf Download Maths Form 4 Paper 2 Questions and Answers Maths Form 4 Past Papers Maths Form 4 Question Papers Maths Form 4 Questions Maths Form 4 Questions and Answers Maths Form 4 Questions and Answers Pdf Maths Form 4 Quiz Maths Form 4 Revision Notes Maths Form 4 Schemes of Work Maths Form 4 Summary Notes Maths Form 4 Syllabus Maths Form 4 Textbook Pdf Maths Form 4 Work Maths Form 5 Chapter 1 Exercise and Answers Maths Form 5 Chapter 1 Notes Pdf Maths Form 5 Chapter 2 Notes Pdf Maths Form 5 Chapter 2 Slideshare Maths Form 5 Chapter 3 Notes Pdf Maths Form 5 Notes Pdf Maths Form Four Book Maths Form Four Notes Maths Form Four Notes and Questions Maths Form Four Notes GCSE Maths Form Four Notes Pdf Maths Form Four Past Papers Maths Form Four Questions Maths Form Four Questions and Answers Maths Form Four Questions and Answers Pdf Maths Form Four Quiz Maths Form Four Study Notes Maths Form Four Syllabus Maths Form Four Topic 2 Maths Form Four Topic 4 Maths Form Four Topics Maths Form Four Work Maths Form One Maths Form One Book Maths Form One Book Pdf Maths Form One Download Topic 1 Upto 3 Maths Form One Exam Maths Form One Notes Maths Form One Notes and Questions Maths Form One Notes GCSE Maths Form One Notes Pdf Maths Form One Pdf Maths Form One Questions Maths Form One Questions and Answers Maths Form One Questions and Answers Pdf Maths Form One Questions and Their Answers Maths Form One Quiz Maths Form One Revision Question Maths Form One Schemes of Work Maths Form One Study Notes Maths Form One Syllabus Maths Form One Term Three Test Maths Form One to Three Notes Maths Form One Work Maths Form Three Maths Form Three Book Maths Form Three Notes Maths Form Three Notes and Questions Maths Form Three Notes GCSE Maths Form Three Questions and Answers Maths Form Three Questions and Answers Pdf Maths Form Three Quiz Maths Form Three Reproduction Maths Form Three Reproduction. Maths Form Three Study Notes Maths Form Three Work Maths Form Three-questions and Answers Maths Form Two Maths Form Two Book Maths Form Two Diagrams Maths Form Two Notes Maths Form Two Notes and Questions Maths Form Two Notes GCSE Maths Form Two Notes Pdf Maths Form Two Notes-pdf Maths Form Two Pdf Maths Form Two Questions Maths Form Two Questions and Answers Maths Form Two Questions and Answers Pdf Maths Form Two Quiz Maths Form Two Study Notes Maths Form Two Topics Maths Form Two Work Maths Form Two,schemes of Work Maths Form2 Maths Form2 Textbook Maths Game Form Four Question End Answers Maths Grade 10 Exam Papers Maths Hsc Pdf Maths Human Reproduction Video Maths IGCSE Past Papers Xtremepapers Maths K.c.s.e 2017 Maths KCSE Maths KCSE 2016 Maths KCSE 2017 Maths KCSE 2017 Paper 1 Maths KCSE Past Papers Maths KCSE Questions Maths KCSE Questions and Answer Maths KCSE Quizzes & Answers Maths KCSE Revision Maths KCSE Revision Notes Maths KCSE Setting Questions Form One and Two Maths Ksce 2015 Maths Last Year K.c.s.e Questions Maths Lesson Plan Form Two Maths Made Familiar Maths Mcq for Class 11 Maths Mcq for Class 12 Maths Mcq for Competitive Exams Maths Mcq for Competitive Exams Pdf Maths Mcq for Neet Pdf Maths Mcq for Ssc Maths Mcq Questions With Answers Maths Mcq With Answers Pdf Maths Mcqs for Class 12 Pdf Maths Mcqs With Answers Pdf Maths Mid Familia Form One Maths Mock Papers Maths Module Form 5 Maths Multiple Choice Questions and Answers Cxc Maths Multiple Choice Questions and Answers Pdf Maths Multiple Choice Questions With Answers Pdf Maths Note Maths Note Form Two All Chapters Maths Notes Maths Notes and Guestion and Answear Maths Notes and Syllabus Maths Notes Class 10 Maths Notes for Class 11 Pdf Maths Notes for Class 12 Pdf Maths Notes for High School Students Maths Notes for IGCSE 2014 Maths Notes Form 1 Maths Notes Form 1 4 Maths Notes Form 1 Free Download Maths Notes Form 1 KLB Maths Notes Form 1 Pdf Maths Notes Form 1-4 Maths Notes Form 1-4(1) Maths Maths Notes Form 14 Maths Notes Form 2 Maths Notes Form 2 KLB Maths Notes Form 2 Pdf Maths Notes Form 2; Maths Notes Maths Notes Form 3 Maths Notes Form 3 KLB Maths Notes Form 3 Pdf Maths Notes Form 4 Maths Notes Form 4 Chapter 2 Maths Notes Form 4 KLB Maths Notes Form 4 Pdf Maths Notes Form 4-pdf Maths Notes Form Four Maths Notes Form Four KLB Maths Notes Form Four Pdf Maths Notes Form One Maths Notes Form One KLB Maths Notes Form One Pdf Maths Notes Form One to Form Four Maths Notes Form Three Maths Notes Form Three KLB Maths Notes Form Three Pdf Maths Notes Form Two Maths Notes Form Two KLB Maths Notes Form Two Pdf Maths Notes Form2 Maths Notes IGCSE Maths Notes Kenya Maths Notes on Agroforestry Maths Notes Pdf Maths Notes: Maths Objective Answer Maths Objective Answer 2018 Maths Objective Questions for Competitive Exams Maths Objective Questions for Competitive Exams Pdf Maths Oral Exam Questions Maths Paper 1 Maths Paper 1 2018 Marking Rules Maths Paper 1 Notes Maths Paper 1 Questions Maths Paper 1 Questions and Answers Maths Paper 1 Topics Maths Paper 1 With Answers Maths Paper 2 Maths Paper 2 2017 Maths Paper 2 2018 Marking Rules Maths Paper 2 Questions and Answers Maths Paper 2 Questions and Answers Pdf Maths Paper 2 Revision Maths Paper 2 Topics Maths Paper 2018 Maths Paper 3 2018 Marking Rules Maths Paper 3 Question and Answer Maths Paper 3 Question Paper 2014 KCSE Maths Paper 3 Question Paper 2015 KCSE Maths Paper 3 Question Paper 2016 KCSE Maths Paper 3 Question Paper 2017 KCSE Maths Paper 3 Question Paper 2018 KCSE Maths Paper 3 Questions and Answers Maths Paper One Questions and Answers Maths Paper One Topics Maths Paper Two Qestions With Answers Maths Paper1 Maths Paper2 Maths Paper3 Maths Paper4 Maths Past Papers Maths Past Papers 2017 Maths Past Papers a Level Maths Past Papers Form 1 Maths Past Papers Form 2 Maths Past Papers Form 3 Maths Past Papers O Level Maths Pdf Download Maths Pp1 KCSE 2016 Maths Practical Book Class 12 Pdf Maths Practical Exam Maths Practicals Form One Maths Practicals Questions and Answers Maths Practice Test 9th Grade Maths Practice Test Answers Maths Practice Test Questions and Answers Maths Practice Test Quizlet Maths Predicted Questions This Year KCSE Maths Preparation Notes Maths Pretest High School Pdf Maths Question and Answer With Explanation Maths Question and Answers 2019 Maths Question and Answers 2021 Maths Question and Answers 2022 Maths Question and Answers 2023 Maths Question and Answers Note Maths Questions Maths Questions and Answers Maths Questions and Answers for High School Maths Questions and Answers for High Schools Maths Questions and Answers for High Schools Pdf Maths Questions and Answers for Secondary Schools Maths Questions and Answers Form 1 Maths Questions and Answers Form 2 Maths Questions and Answers Form 3 Maths Questions and Answers Form 4 Maths Questions and Answers Multiple Choice Maths Questions and Answers Notes Maths Questions and Answers O Maths Questions and Answers Online Maths Questions and Answers Pdf Maths Questions and Answers Pdf for Class 12 Maths Questions and Answers Pdf for Competitive Exams Maths Questions and Answers-form 2 Maths Questions for High School Maths Questions for High School Students With Answers Maths Questions for Senior 1 Maths Questions for Senior 2 Maths Questions for Senior 3 Maths Questions for Senior 4 Maths Questions for Senior 5 Maths Questions for Senior 6 Maths Questions for Senior Five Maths Questions for Senior Four Maths Questions for Senior One Maths Questions for Senior Six Maths Questions for Senior Three Maths Questions for Senior Two Maths Questions Form One Maths Questions Multiple Choice Maths Questions Quizlet Maths Questions to Ask Your Teacher Maths Quetion and Answer Form Four Maths Quetion and Answer Form One Maths Quetion and Answer Form Three Maths Quetion and Answer Form Two Maths Quiz for Class 9 Maths Quiz for Class 9 Maths Maths Quiz Questions and Answers for Class 10 Maths Quiz Questions and Answers for Class 10 Pdf Maths Quiz Questions and Answers for Class 12 Maths Quiz Questions and Answers for Class 9 Maths Quiz Questions and Answers for Class 9 Pdf Maths Quiz Questions and Answers for High School Maths Quiz Questions and Answers Multiple Choice Maths Quiz Questions and Answers Pdf Maths Quiz Questions for Class 12 Maths Quiz Questions for College Students Maths Quiz With Answers Maths Quiz With Answers Pdf Maths Quizlet Maths Revision Maths Revision a Level Maths Revision Maths Notes Maths Maths Revision Exam Maths Revision Examination Maths Revision Form One Maths Revision Notes Maths Revision Notes Maths Maths Revision Notes Form 1 Maths Revision Notes Form 2 Maths Revision Notes Form 3 Maths Revision Notes Form 4 Maths Revision Notes IGCSE Maths Revision Paper One Maths Revision Questions Maths Revision Questions and Answers Maths Revision Questions and Answers Form 1 Maths Revision Questions and Answers Form 2 Maths Revision Questions and Answers Form 3 Maths Revision Questions and Answers Form 4 Maths Revision Questions and Answers Form Four Maths Revision Questions and Answers Form One Maths Revision Questions and Answers Form Three Maths Revision Questions and Answers Form Two Maths Revision Questions Form 1 Maths Revision Questions Form 2 Maths Revision Questions Form 3 Maths Revision Questions Form 4 Maths Revision Questions Form Four Maths Revision Questions Form One Maths Revision Questions Form Three Maths Revision Questions Form Two Maths Revision Quiz Maths Revision Test Maths Secondary School Revision Maths Simple Notes Maths Spm Notes Download Maths Spm Notes Pdf Maths Spm Questions Maths Study Form 2 Maths Study Guide Maths Study Guide Answer Key Maths Study Guide Answers Maths Study Guide Maths Questions and Answers Maths Study Guide Ib Maths Study Guide Pdf Maths Study Guides Maths Study Notes Maths Study Notes Materials Form 1 Pdf Maths Study Notes Materials Form 2 3 Pdf Maths Study Notes Materials Form 2 Pdf Maths Study Notes Materials Form 3 Pdf Maths Study Notes Materials Form 4 Pdf Maths Syllabus in Kenya Maths Syllabus Pdf Maths Test 1 Quizlet Maths Test Questions Maths Test Questions and Answers Maths Test Questions and Answers Pdf Maths Topic One Form Four Maths Topics Form One Maths Unit 1 Quiz Maths Vol 3 Maths | Revision Maths Maths,form 4 Maths.form Four.topic Three MathsExam Form Three MathsModule Form 5 MathsNotes MathsNotes for Class 11 Pdf MathsNotes for Class 12 Pdf MathsNotes Form 1 MathsNotes Form 1 Free Download MathsNotes Form 2 MathsNotes Form 3 MathsNotes Form 3 Pdf MathsNotes IGCSE MathsNotes Pdf MathsPast Papers MathsQuestions and Answers Pdf MathsSimple Notes MathsSpm Notes Download MathsSpm Notes Pdf MathsSpm Questions MathsStudy Guide Answers MathsStudy Guide Pdf MathsStudy Guides Blologytextpapers Bridge Maths Business Past KCSE Past Papers Maths Form 3 Notes Pdf Maths Form 4 Notes Pdf C R E Form One KLB C R E Form One Oli Topic C.r.e Form 1 Notes Kenya C.r.e Form 2 Notes Kenya C.r.e Form 3 Notes C.r.e Form 3 Notes Kenya C.r.e Form 3 Pdf C.r.e Form 4 Notes Kenya C.r.e Form One Notes Pdf C.r.e Notes Form 1 C.r.e Revision Notes C.r.e Short Notes Cambridge IGCSE Maths Cambridge IGCSE Maths 3rd Edition Cambridge IGCSE Maths 3rd Edition Plus Cd South Asia Edition Cambridge IGCSE Maths Answers Cambridge IGCSE Maths Coursebook Pdf Download Cambridge IGCSE Maths Practical Workbook Cambridge IGCSE Maths Revision Guide Pdf Cambridge IGCSE Maths Study and Revision Guide 2nd Edition Pdf Cambridge IGCSE Maths Study and Revision Guide Pdf Cambridge IGCSE Maths Workbook Free Download Cambridge IGCSE Maths Workbook Pdf Cambridge IGCSE® Maths Coursebook Caucasian Chalk Circle Essay Questions Chapter 1 Introduction to Maths Chapter 1 Introduction to Maths Studies Cie a Level Maths Notes 2016 Cie a Level Maths Notes Pdf Cie Past Papers Class 10 Maths Chapter 1 Mcqs Class 8 Maths Notes KCSE-kcse College Maths Notes College Maths Practice Test College Maths Quiz College Maths Quiz Chapter 1 College Maths Quizlet College Maths Study Guide College Maths Study Guide Pdf College Maths Test Questions and Answers College Maths Volume 3 Pdf College MathsNotes Complete Maths for Cambridge IGCSE Complete Maths for Cambridge IGCSE Revision Guide Pdf County Mocks 2017 Cse Past Papers Maths 2017 Dl Maths Form 3 Pdf Kusoma Download Maths Form 1 Download Maths Form 2 Download Maths Form 2 Notes Download Maths Form 3 Download Maths Form 3 Notes Download Maths Form 4 Download Maths Form Four Download Maths Form One Download Maths Form Three Download Maths Form Two Download Maths Notes Form 3 Download Maths Notes Form One Download MathsNotes Form 3 Download Form Three Maths Notes Download Free KCSE Past Papers Maths Download Free KCSE Past Papers From KNEC. Download KCSE Past Papers With Answers Download KCSE Revision Notes Download KLB Maths Book 2 Download KLB Maths Book 3 Download KLB Maths Book 4 Download Notes of Maths Downloads | Maths | Form Four Exams | Exams Downloads | Maths | Form One Exams | Exams Downloads | Maths | Form Three Exams | Exams Downloads | Maths | Form Two Exams | Exams Downloads | KCSE Papers and Marking Schemes | Dvance KCSE Past Papers Easy Maths Questions Edexcel a Level Maths B Edexcel a Level Maths Notes Pdf Edexcel a Level Maths Salters Nuffield Edexcel A2 Maths Notes Edexcel as Maths Revision Guide Pdf Edexcel Maths A2 Revision Notes Pdf Edexcel Maths Unit 2 Revision Notes Edexcel GCSE Maths Revision Guide Pdf Edexcel IGCSE Maths Past Papers Edexcel IGCSE Maths Revision Guide Free Pdf Download Edexcel IGCSE Maths Revision Guide Pdf Edexcel IGCSE Maths Revision Guide Pdf Download Electronics Form Four Notes Energy Questions Maths Bowl Essay Questions and Answers KCSE Maths Notes Essay Questions and Answers on Betrayal in the City Essay Questions Based on Betrayal in the City Evolving World Maths Book 1 Pdf Evolving World Maths Book 4 Notes Evolving World Maths Book Form 1 Evolving World-history Book 3 Exam Notes for Maths 101 Exams KCSE Maths Paper 1 Questions and Answers F3 Maths Test Paper Find Download KCSE Past Papers With Answers Find KCSE Maths Essay Questions and Answers Form 1 Maths Exam Form 1 Maths Notes Form 1 Maths Questions and Answers Form 1 Maths Questions and Answers Pdf Form 1 Maths Revision Notes Form 1 Maths Summurized Revision Pdf Form 1 Maths Syllabus Form 1 Maths Test Paper Pdf Form 1 Maths Topics Form 1 MathsNotes Form 1 MathsQuestions and Answers Form 1 MathsRevision Notes Form 1 MathsSyllabus Form 1 MathsTest Paper Pdf Form 1 Past Papers Form 1 Past Papers With Answers Form 1 Revision Papers Form 1 Subjects in Kenya Form 2 Maths Exam Form 2 Maths Exam Paper Form 2 Maths Exam Paper 2016 Form 2 Maths Exam Paper Free Download Form 2 Maths Exam Paper With Answer Form 2 Maths Final Year Exam Paper 2 Form 2 Maths Notes Form 2 Maths Notes and Revision Questions Form 2 Maths Notes Pdf Form 2 Maths Past Papers Form 2 Maths Questions Form 2 Maths Questions and Answers Form 2 Maths Questions and Answers > Form 2 Maths Questions and Answers Pdf Form 2 Maths Revision Notes Form 2 Maths Short Notes Form 2 Maths Syllabus Form 2 MathsExam Paper Form 2 MathsExam Paper Free Download Form 2 MathsExam Paper With Answer Form 2 MathsFinal Year Exam Paper 2 Form 2 MathsPast Papers Form 2 MathsRevision Notes Form 2 MathsShort Notes Form 2 MathsSyllabus Form 2 Revision Papers Form 2 Subjects in Kenya Form 3 Maths Book Form 3 Maths Exam Form 3 Maths Exam Paper Form 3 Maths Notes Form 3 Maths Past Papers Form 3 Maths Questions Form 3 Maths Questions and Answers Form 3 Maths Questions and Answers Pdf Form 3 Maths Revision Notes Form 3 Maths Syllabus Form 3 MathsExam Paper Form 3 MathsNotes Form 3 MathsPast Papers Form 3 MathsQuestions Form 3 MathsQuestions and Answers Pdf Form 3 MathsRevision Notes Form 3 MathsSyllabus Form 3 C.r.e Form 3 Notes of Maths Topic on Fish Form 3 Past Papers Form 3 Revision Papers Form 3 Subjects in Kenya Form 4 Maths Exam Form 4 Maths Notes Form 4 Maths Notes Pdf Form 4 Maths Questions and Answers Form 4 Maths Questions and Answers Pdf Form 4 Maths Revision Notes Form 4 Maths Syllabus Form 4 Maths Topics Form 4 MathsNotes Form 4 MathsRevision Notes Form 4 MathsSyllabus Form 4 MathsTopics Form 4 Exam Papers Form 4 Revision Papers Form 4 Subjects in Kenya Form 5 Maths Topics Form 5 MathsTopics Form Five Maths Notes Form Five MathsNotes Form Four Maths Book Form Four Maths Notes Form Four Maths Notes Pdf Form Four Maths Questions and Answers Form Four Maths Questions and Answers Pdf Form Four Maths Revision Questions Form Four Maths Syllabus Form Four Maths Topics Form Four MathsNotes Form Four MathsQuestions and Answers Form Four MathsQuestions and Answers Pdf Form Four MathsTopics Form Four Notes Form Four Revision Papers Form Four Subjects in Kenya Form One Maths Book Form One Maths Examination Form One Maths First Topic Form One Maths Lesson Plan Form One Maths Notes Pdf Form One Maths Past Papers Pdf Form One Maths Questions Form One Maths Questions and Answers Form One Maths Questions and Answers Pdf Form One Maths Revision Questions Form One Maths Short Notes Form One Maths Syllabus Form One Maths Topics Form One MathsExamination Form One MathsPast Papers Pdf Form One MathsQuestions and Answers Form One MathsQuestions and Answers Pdf Form One MathsTopics Form One Exams Form One Notes of Maths Form One Past Papers Form One Subjects in Kenya Form One Term One Maths Exam Form One Term One MathsExam Form Three Maths Book Form Three Maths Book Pdf Form Three Maths Notes Form Three Maths Notes Pdf Form Three Maths Questions and Answers Form Three Maths Questions and Answers Pdf Form Three Maths Revision Questions Form Three Maths Syllabus Form Three Maths Topics Form Three MathsNotes Form Three MathsNotes Pdf Form Three MathsQuestions and Answers Form Three MathsQuestions and Answers Pdf Form Three MathsTopics Form Three Subjects in Kenya Form Two Maths Book Form Two Maths Cat Form Two Maths Examination Form Two Maths Notes Form Two Maths Notes Pdf Form Two Maths Past Papers Form Two Maths Questions and Answers Form Two Maths Questions and Answers Pdf Form Two Maths Revision Questions Form Two Maths Syllabus Form Two Maths Topics Form Two MathsNotes Form Two MathsNotes Pdf Form Two MathsQuestions and Answers Form Two MathsQuestions and Answers Pdf Form Two MathsSyllabus Form Two MathsTopics Form Two Notes Form Two Subjects in Kenya Free a-level Maths Revision App | Pass Your Maths Exams Free Maths Form 1 Notes Free Maths Notes Form 1 Free Maths Notes Pdf Free MathsNotes Pdf Free College Maths Practice Test Free Form1,form2,form3 Past Papers Free KCSE Past Papers Free KCSE Mocks 2015 Free KCSE Past Papers 2014 Free KCSE Past Papers KCSE Past Free KCSE Past Papers Kenya, Free KCSE Past Papers With Answers Free KCSE Questions and Answers on Maths Free KCSE Revision Notes Free Marking Schemes Free Mocks Online KCSE Answers Past Exams Question Papers Free Revision Papers From Three Notes Topic One KLB Fun Maths Questions Funny Maths Questions Funny Maths Questions and Answers Funny Maths Questions to Ask Funny Maths Quotes GCSE Maths Exam Questions and Answers GCSE Maths Past Papers GCSE Maths Revision GCSE Maths Revision Notes GCSE Maths Revision Notes Pdf GCSE Maths Revision Notes Pdf 9-1 GCSE Maths Revision Questions and Answers GCSE Maths Textbook Pdf GCSE Maths Topics Pass My Exams: Easy Exam Revision Notes Home Maths Notes Pdf Home Maths Practice Test With Answers Home Maths Quiz Home Maths Quiz Pdf Home Maths Test Questions and Answers Home Maths Test Questions and Answers Pdf Home Knowledge in Maths Human Body Good Maths Questions to Ask GRE Maths Practice Test GRE Maths Subject Test Pdf Handbook of Maths Pdf Free Download Hard Maths Questions Hard Maths Questions and Answers Hard Maths Questions to Ask Your Teacher Hard Maths Quiz Questions Hard Form 3 Maths Question High School Maths Final Exam Doc High School Maths Final Exam Pdf High School Maths Final Exam Questions High School Maths Final Exam Questions and Answers High School Maths Notes High School Maths Practice Test High School Maths Pretest With Answers High School Maths Questions and Answers Pdf High School Maths Study Guide High School Maths Test Questions and Answers Pdf High School MathsNotes High School MathsStudy Guide How to Answer KCSE Maths Question How to Motivate a Form 4 Student How to Motivate a KCSE Candidate How to Motivate a KCSE Student How to Pass Maths Questions & Answers Form 1&2 | Text Book How to Revise Maths How to Revise Effectively for KCSE How to Study Maths: 5 Study Techniques to Master Maths Hsc Maths 2018 Hsc Maths 2019 Https://www.knec.ac.ke/ Www.knec-portal.ac.ke/ KNEC Portal: Ial Maths Notes Ib Maths Cold War Notes Ib Maths Notes Ib Maths Notes Pdf Ib Maths of the Americas Notes Ib Maths of the Americas Study Guide Ib Maths Paper 2 Study Guide Ib Maths Question Bank by Topic Ib Maths Study Guide Pdf Ict Notes Form 1 IGCSE Maths Alternative to Practical Revision IGCSE Maths Alternative to Practical Revision Notes IGCSE Maths Book IGCSE Maths Book Pdf Download IGCSE Maths Notes IGCSE Maths Notes 2017 Pdf IGCSE Maths Notes Edexcel IGCSE Maths Paper 2 Notes IGCSE Maths Paper 6 Notes IGCSE Maths Past Papers IGCSE Maths Past Papers 2014 IGCSE Maths Past Papers 2017 IGCSE Maths Pdf IGCSE Maths Pre Release Material 2018 IGCSE Maths Resources IGCSE Maths Revision Guide IGCSE Maths Revision Guide Free Download IGCSE Maths Revision Guide Pdf Download IGCSE Maths Revision Notes Pdf IGCSE Maths Revision Worksheets IGCSE Maths Workbook Pdf IGCSE Maths Znotes IGCSE MathsPast Papers IGCSE Notes Maths Importance of Agroforestry Inorganic Maths Multiple Choice Questions With Answers Pdf Inorganic Maths Questions and Answers Pdf Interesting Maths Questions Interesting Maths Questions and Answers Interesting Questions to Ask About Maths Intro to Maths Quiz Introduction of Maths Form One Introduction to Maths Introduction to Maths Notes Introduction to Maths Pdf Introduction to MathsNotes Is Agroforestry Sustainable? K.c.s.e Answers Maths Paper One 2018 K.c.s.e Maths 2017 K.c.s.e Maths 2018 K.c.s.e Maths Paper 1 2017 K.c.s.e Mocks 2018 K.c.s.e Papers 2015 K.c.s.e Papers 2016 K.c.s.e Past Papers 2014 K.c.s.e.Maths Paper 2 Year 2018 K.c.s.e.results 2018 for Busia County K.l.b Maths Form 3 K.l.b Maths Notes K.l.b MathsNotes Kasneb Past Papers for Colleges Maths Past Papers KCSE 2010 Marking Scheme KCSE 2010 Past Papers KCSE 2011 Maths Paper 1 KCSE 2011 Marking Scheme KCSE 2012 Maths Paper 2 Marking Scheme KCSE 2012 Marking Schemes KCSE 2013 Maths Paper 1 KCSE 2013 Marking Scheme KCSE 2013 Marking Scheme Pdf KCSE 2014 KCSE 2015 Maths Paper 2 KCSE 2015 Maths Paper 3 KCSE 2015 Marking Scheme KCSE 2015 Past Papers KCSE 2016 Maths Paper 1 KCSE 2016 Maths Paper 2 KCSE 2017 Maths Paper 1 KCSE 2017 Maths Paper 2 KCSE 2017 Hostory Papers With Answers.com KCSE 2017 Marking Scheme KCSE 2017 Papers KCSE 2017 Papers and Marking Scheme KCSE 2017 Papers Pdf KCSE 2017 Past Papers KCSE 2017 Prediction Pdf KCSE 2018 Maths and Answers KCSE 2018 Maths Prediction KCSE 2018 Leakage KCSE 2018 Marking Scheme KCSE 2018 Papers KCSE 2018 Prediction Pdf KCSE 2018 Predictions KCSE 2018 Questions KCSE 2018 Questions and Answers KCSE 2019 Leakage Maths KCSE 2019 Marking Scheme KCSE 2019 Questions KCSE 2019 Questions and Answers KCSE 2021 Questions KCSE 2021 Questions and Answers KCSE Answers KCSE Answers Past Exams Question Papers Downloads | KCSE Maths 2011 KCSE Maths 2016 KCSE Maths Diagramsbiology Revision Tips KCSE Maths Essay Questions and Answers KCSE Maths Essay Questions and Answers Pdf KCSE Maths Essays KCSE Maths Essays Pdf KCSE Maths Marking Schemes KCSE Maths Notes KCSE Maths Notes Pdf KCSE Maths Notes, Syllabus, Questions, Answers KCSE Maths Paper 1 KCSE Maths Paper 1 2011 KCSE Maths Paper 1 2012 KCSE Maths Paper 1 2013 KCSE Maths Paper 1 2015 KCSE Maths Paper 1 2016 KCSE Maths Paper 1 2017 KCSE Maths Paper 1 2017 Pdf KCSE Maths Paper 1 Questions and Answers KCSE Maths Paper 2 KCSE Maths Paper 2 2012 KCSE Maths Paper 2 2012 KCSE Maths Paper 2 2015 KCSE Maths Paper 2 2013 KCSE Maths Paper 2 2014 KCSE Maths Paper 2 2015 KCSE Maths Paper 2 2016 KCSE Maths Paper 2 2017 KCSE Maths Paper 3 KCSE Maths Paper 3 2012 KCSE Maths Paper 3 2016 KCSE Maths Paper 3 2017 KCSE Maths Paper 3 Past Papers KCSE Maths Past Papers KCSE Maths Past Papers and Answers KCSE Maths Past Papers Pdf KCSE Maths Practical KCSE Maths Practical 2015 KCSE Maths Practical 2016 KCSE Maths Practical Past Papers KCSE Maths Practicals KCSE Maths Practicals KCSE Maths Paper 1 KCSE Maths Question and Answer KCSE Maths Questions and Answers KCSE Maths Questions and Answers Ap Maths KCSE Maths Revision KCSE Maths Revision Notes KCSE Maths Revision Papers KCSE Maths Revision Questions KCSE Maths Revision Questions and Answers KCSE Maths Syllabus KCSE MathsNotes KCSE MathsPaper 1 KCSE MathsPaper 2 KCSE MathsPaper 2 Pdf KCSE MathsSyllabus KCSE Business Paper 1 2016 KCSE Business Past Papers KCSE Maths Past Papers KCSE Essay Questions in Betrayal in the City KCSE Essays KCSE Exam Papers 2018 KCSE Exam Papers Answers KCSE Form 1 Maths Revision KCSE Form 2 Maths Revision KCSE Form 3 Maths Revision KCSE Form 4 Maths Revision KCSE Form Four Maths Revision KCSE Form One Maths Revision KCSE Form Three Maths Revision KCSE Form Two Maths Revision KCSE KCSE Past Papers KNEC KCSE Leakage KCSE Leakage Maths KCSE Made Familiar Maths KCSE Made Familiar Maths Pdf KCSE Marking Scheme 2016 KCSE Marking Schemes KCSE Marking Schemes 2017 KCSE Marking Schemes Pdf KCSE Mock Exams KCSE Mock Papers 2015 KCSE Mock Papers 2017 KCSE Mock Papers 2018 KCSE Mock Papers Pdf KCSE Mock Papers Pdf 2018 KCSE Mock Papers Pdf KCSE Past Papers KCSE Mocks 2017 KCSE Mocks 2018 KCSE Notes KCSE Online Notes KCSE Online Past Papers KCSE Online Registration KCSE Papers 2015 KCSE Papers and Marking Schemes | Exams KCSE Past Papers KCSE Past Papers 2007 KCSE Past Papers 2009 KCSE Past Papers 2010 KCSE Past Papers 2011 KCSE Past Papers 2011 Pdf KCSE Past Papers 2012 KCSE Past Papers 2013 KCSE Past Papers 2013knec KCSE Past Papers 2014 KCSE Past Papers 2014 Pdf KCSE Past Papers 2015 KCSE Past Papers 2015 Marking Schemes KCSE Past Papers 2015 Pdf KCSE Past Papers 2016 KCSE Past Papers 2016 Pdf KCSE Past Papers 2017 KCSE Past Papers 2017 Pdf KCSE Past Papers 2018 KCSE Past Papers Maths KCSE Past Papers Maths and Answers KCSE Past Papers Maths Pdf KCSE Past Papers Maths With Answers KCSE Past Papers Mathsand Answers KCSE Past Papers Maths and Answers KCSE Past Papers KCSE and Answers KCSE Past Papers KCSE and Answers Free Mocks Online KCSE Past Papers Marking Scheme KCSE Past Papers Pdf Download KCSE Past Papers Pdf Download KCSE 2013 KCSE Past Papers With Answers KCSE Past Papers Woodwork and Answers KCSE Prediction 2017 KCSE Prediction 2018 KCSE Prediction 2018 Pdf KCSE Prediction Papers 2018 KCSE Prediction Questions KCSE Prediction Questions 2018 KCSE Prediction Questions and Answers KCSE Questions KCSE Questions and Answers KCSE Questions and Answers. KCSE Questions on Maths KCSE Results, Online Registration, KCSE Result Slip. KCSE Revision KCSE Revision Notes KCSE Revision Notes Maths KCSE Revision Notes Pdf KCSE Revision Papers KCSE Revision Papers 2014 KCSE Revision Papers With Answers KCSE Revision Question for Maths KCSE Revision Questions KCSE Revision Questions and Answers KCSE Revision | Secondary School | Text Books | Text Book Centre KCSE Syllabus Pdf KCSE Trial 2017 KCSE Trial Exams 2017 Kenya Secondary School Maths Syllabus Kenya Secondary School Maths Syllabus Pdf Kenya Secondary School MathsSyllabus Pdf Kenya Secondary School Syllabus Pdf Kenya-kcse-christian Religious Education Syllabus Kenyaplex KCSE Past Papers Kenyaplex Past Papers for Secondary KLB Maths Book 1 Download KLB Maths Book 1 Notes KLB Maths Book 1 Pdf KLB Maths Book 2 KLB Maths Book 2 Notes KLB Maths Book 2 Notes Pdf KLB Maths Book 2 Pdf KLB Maths Book 3 Notes KLB Maths Book 3 Pdf KLB Maths Book 3 Pdf Download KLB Maths Book 4 Notes KLB Maths Book 4 Pdf KLB Maths Book 4 Pdf Download KLB Maths Book 4 Topics KLB Maths Book One KLB Maths Form 1 KLB Maths Form 1 Notes KLB Maths Form 1 Pdf KLB Maths Form 2 KLB Maths Form 2 Book KLB Maths Form 2 Notes KLB Maths Form 2 Pdf KLB Maths Form 2 Pdf Download KLB Maths Form 2 Schemes of Work KLB Maths Form 3 KLB Maths Form 3 Notes KLB Maths Form 3 Notes Pdf KLB Maths Form 3 Pdf KLB Maths Form 3 Pdf Download KLB Maths Form 4 KLB Maths Form 4 Notes KLB Maths Form 4 Pdf KLB Maths Form Four KLB Maths Form Four Notes KLB Maths Form One KLB Maths Form One Notes KLB Maths Form Three KLB Maths Form Three Notes KLB Maths Form Two KLB Maths Form Two Notes KLB Maths Notes KLB Maths Notes Form 4 KLB Maths Pdf KLB MathsNotes KLB MathsNotes Form 4 KLB MathsPdf KNEC Maths Syllabus KNEC Examiners Portal KNEC Website KNEC Ict Past Papers KNEC Past Papers for Colleges KNEC Past Papers Free Download KNEC Past Papers Free Downloads KNEC Past Papers Pdf KNEC Portal Confirmation KNEC Portal KCSE Results KNEC Portal KNEC Past Papers for Colleges Kasneb Past Papers KNEC Revision Papers KNEC Technical Exams Past Papers Kusoma Maths Notes Kusoma Maths Notes Pdf Kusoma Notes Maths Kusoma.co.ke Kusoma.com Past Papers Learner Guide for Cambridge IGCSE Maths Longhorn Maths Book 3 Pdf Made Familiar Maths Made Familiar Maths Pdf Made Familiar Maths Questions Maktaba Tetea Notes Marking Scheme KCSE Maths Past Papers Math Form2 Note Mcqs About Gaseous Exchange Middle School Maths Bowl Maths Questions Mock Past Papers 2017 Mock Past Papers With Answers Mokasa Mock 2017 More Than 1800 Maths Questions and Answers to Help You Study Multiple Choice Questions on Maths Necta Maths Past Papers Necta Maths Practicals Necta MathsPast Papers Necta MathsPracticals Necta Form Four Past Papers Necta Past Papers Form 4 Necta Past Papers Form 4 2016 Necta Past Papers Form Six Necta Past Papers Form Two Necta Questions and Answers Necta Review Questions Notes Maths Form 1 Notes Maths Form 2 Notes Maths Form 3 Notes Maths Form 3 Notes Pdf Notes Maths Form 3 Syllabus Notes Maths Form 4 Syllabus Notes on Maths Studies Notes Za Maths 4m 2 Notes Za Maths Form One Notes Za Maths Form Three O Level Maths Practical Experiments O Level Maths Questions and Answers Pdf Orm Three Maths Notes Papacambridge Maths IGCSE Papers KNEC KCSE Online Past Papers KNEC KCSE Results Past Papers Past KCSE Papers Past Paper Questions by Topic Maths Past Papers 2014 Past Papers in Kenya Pdf Maths Form 3 Pdf Maths Notes Pdf Maths Notes Form 1 Pdf Maths Notes Form 2 Pdf Maths Notes Form 3 Pdf Maths Notes Form 4 Pdf Maths Notes Form Four Pdf Maths Notes Form One Pdf Maths Notes Form Three Pdf Maths Notes Form Two Pdf Form 1 Maths Questions and Answers Pdf Form 2 Maths Questions and Answers Pdf Form 3 Maths Questions and Answers Pdf Form 4 Maths Questions and Answers Pdf Form Four Maths Questions and Answers Pdf Form One Maths Questions and Answers Pdf Form Three Maths Questions and Answers Pdf Form Two Maths Questions and Answers Pdf Free KCSE Past Papers and Marking Schemes Pdf" Revision Questions Maths Form 1 Practical Maths Experiments Pdf Practical Maths Question and Answer Pdf Pre Mocks 2018 Preliminary Maths Pte KNEC Past Papers Questions and Answers Pdf Maths Form 1 Questions and Answers Pdf Maths Form 2 Questions and Answers Pdf Maths Form 3 Questions and Answers Pdf Maths Form 4 Questions and Answers Pdf Maths Form Four Questions and Answers Pdf Maths Form One Questions and Answers Pdf Maths Form Three Questions and Answers Pdf Maths Form Two Questions Based to Introduction to Maths Questions on Gaseous Exchange in Humans Questions on Introduction to Maths Questions to Ask in Maths Class Questions to Confuse Your Maths Teacher Quizlet Maths Test Quizlet Test Questions Qustions in Maths and Answers Revision Revision Maths Notes and Questions? Revision Quiz for Maths for Form Three S.1 Maths Questions S.2 Maths Questions S.3 Maths Questions S.4 Maths Questions School Maths Notes Secondary Maths Notes Secondary Maths Notes Pdf Secondary MathsNotes Pdf Senior 1 Maths Notes Senior 2 Maths Notes Senior 3 Maths Notes Senior 4 Maths Notes Senior 5 Maths Notes Senior 6 Maths Notes Senior Five Maths Notes Senior Four Maths Notes Senior One Maths Notes Senior Six Maths Notes Senior Three Maths Notes Senior Two Maths Notes Simple Scientific Questions Smart Questions to Ask a Maths Teacher Snab Maths Revision Notes Southwest Mock Paper 2 2016 Maths Only Spm Maths Revision Notes Spm Notes Success Maths Spm Pdf Success MathsSpm Pdf Summary of Maths Form 3 Tahossa Past Papers To Motivate a Form 4 KCSE Student To Motivate a Form 4 Student Topical Revision Material Tricky Maths Questions and Answers Tricky Maths Questions for Adults Tricky Maths Questions With Answers Tricky Maths Quiz Questions Two Maths Revision Questions University Maths Volume 3 Openstax University Maths Volume 3 Pdf University Maths Volume 4 Pdf Ur Revision Guide IGCSE Maths Www.Maths Form One Notes.com Www.Maths From One KLB.com Www.form 1 Maths.com Www.form 2 Maths.com Www.form 3 Maths.com Www.form 4 Maths.com Www.form Four Maths.com Www.form One Maths.com Www.form Three Maths.com Www.form Two Maths.com Www.kusoma Notes Www.kusoma Revision Materials Www.kusoma.co.ke Maths Notes Xtremepapers IGCSE Maths Year 11 Maths Z Notes Maths IGCSE Znotes as Maths 2018 Mathematics Paper One Questions and Answers 2018 Mathematics Paper Two Questions and Answers Advice to KCSE Candidates Best Revision Books for KCSE How to Pass an Exam Successfully How to Pass KCSE 2018 How to Pass KCSE 2019 How to Pass KCSE Mathematics Paper How to Pass KCSE Mathematics How to Pass KCSE Mathematics How to Pass KCSE 2019 K.c.s.e Mathematics Paper 1 2017 KCSE 2019 Prediction KCSE Prediction 2019 KCSE Revision Tips KCSE Mathematics Paper 1 2018 KCSE Mathematics Paper 2 2018 KCSE Mathematics Past Papers Pdf KCSE Past Papers 2012 KCSE Past Papers 2017 Pdf KCSE Past Papers 2018 KCSE Past Papers of Mathematics Pp2 KCSE Mathematics Past Papers Pdf Advice to KCSE Candidates Best Revision Books for KCSE How to Pass an Exam Successfully How to Pass KCSE 2018 How to Pass KCSE 2019 How to Pass KCSE Maths Paper How to Pass KCSE Maths How to Pass KCSE Maths How to Pass KCSE 2019 K.c.s.e Maths Paper 1 2017 KCSE 2019 Prediction KCSE Prediction 2019 KCSE Revision Tips KCSE Maths Paper 1 2018 KCSE Maths Paper 2 2018 KCSE Maths Past Papers Pdf KCSE Past Papers 2012 KCSE Past Papers 2017 Pdf KCSE Past Papers 2018 KCSE Past Papers of Maths Pp2 KCSE Maths Past Papers Pdf Maths KCSE Papers With Their Marking Schemes Maths Paper 1 and Answers KCSE 2017 Papers and Marking Scheme KCSE 2019 Papers and Marking Scheme KCSE Maths Paper 1 2018 KCSE Maths Paper 1 2019 KCSE Maths Paper 1 2019 Past Papers KCSE Maths Paper 2 2017 KCSE Maths Paper 2 2018 KCSE Maths Paper 2 2019 KCSE Maths Paper 2 2019 Past Papers KCSE Maths Paper 3 2019 Past Papers KCSE Maths Past Papers and Answers KCSE Marking Schemes Pdf KCSE Past Papers 2015 Marking Schemes KCSE Past Papers 2019 Marking Schemes KCSE Past Papers Maths Paper 1 2019 KCSE Past Papers Maths Paper 2 2019 KCSE Past Papers Maths Paper 3 2019 Past Papers KCSE Maths Paper 1 2019 Past Papers KCSE Maths Paper 2 2019 Past Papers KCSE Maths Paper 3 2019 Mathematics KCSE Papers With Their Marking Schemes Mathematics Paper 1 and Answers KCSE 2017 Papers and Marking Scheme KCSE 2019 Papers and Marking Scheme KCSE Mathematics Paper 1 2018 KCSE Mathematics Paper 1 2019 KCSE Mathematics Paper 1 2019 Past Papers KCSE Mathematics Paper 2 2017 KCSE Mathematics Paper 2 2018 KCSE Mathematics Paper 2 2019 KCSE Mathematics Paper 2 2019 Past Papers KCSE Mathematics Paper 3 2019 Past Papers KCSE Mathematics Past Papers and Answers KCSE Marking Schemes Pdf KCSE Past Papers 2015 Marking Schemes KCSE Past Papers 2019 Marking Schemes KCSE Past Papers Mathematics Paper 1 2019 KCSE Past Papers Mathematics Paper 2 2019 KCSE Past Papers Mathematics Paper 3 2019 Past Papers KCSE Mathematics Paper 1 2019 Past Papers KCSE Mathematics Paper 2 2019 Past Papers KCSE Mathematics Paper 3 2019 KCSE Mathematics Paper 1 2017 KCSE Mathematics Paper 1 2018 KCSE Mathematics Paper 2 2016 KCSE Mathematics Paper 2 2017 Marking Scheme KCSE Mathematics Paper 2 2018 KCSE Mathematics Paper 2 2018 Pdf KCSE Mathematics Past Papers Pdf KCSE Past Papers of Mathematics Pp2 Maths KCSE 2017 K.C.S.E. Paper 1 Maths Revision Calculations KCSE Maths Paper 1 2018 KCSE Mathematics Paper 1 2017 KCSE Mathematics Paper 1 Topics KCSE Mathematics Paper 2 2018 KCSE Mathematics Paper 2 2018 Marking Scheme KCSE Mathematics Paper 2 2018 Pdf KCSE Mathematics Past Papers Pdf Solving Problems Mathematics Paper 1 Pdf Mathematics Form 1 Questions and Answers Mathematics Paper 1 2018 Mathematics Paper 2 2018 Mathematics Paper 1 2019 Mathematics Paper 2 2019 Mathematics Paper 1 Notes Mathematics Paper 1 Questions and Answers Pdf Mathematics Paper 2 Questions and Answers Mathematics Questions and Answers Form 2 KCSE Mathematics Paper 1 2018 KCSE Mathematics Paper 2 2018 KCSE Mathematics Paper 1 2017 KCSE Mathematics Paper 2 2017 KCSE Mathematics Paper 1 2019 KCSE Mathematics Paper 2 2019 Most Tested KCSE Mathematics Questions Maths Form 1 Questions and Answers Maths Paper 1 2018 Maths Paper 2 2018 Maths Paper 1 2019 Maths Paper 2 2019 Maths Paper 1 Notes Maths Paper 1 Questions and Answers Pdf Maths Paper 2 Questions and Answers Maths Questions and Answers Form 2 KCSE Maths Paper 1 2018 KCSE Maths Paper 2 2018 KCSE Maths Paper 1 2017 KCSE Maths Paper 2 2017 KCSE Maths Paper 1 2019 KCSE Maths Paper 2 2019 Most Tested KCSE Maths Questions 4m1 Notes Viusasa 4m2 Notes Viusasa 4m3 Notes Viusasa 4m4 Notes Viusasa Download on Viusasa - Download Now for Free Elimu - Viusasa Elimu Library | Notes, Exams, Lesson Plans, Schemes Elimu Online High School Notes - Revision Materials for Kenyan Schools Https //www.viusasa.com/elimu Kenya Notes Viusasa Elimu Form 1 Notes Viusasa Elimu Form 2 Notes Viusasa Elimu Form 3 Notes Viusasa Elimu Form 4 Notes Viusasa Elimu Form Four Notes Viusasa Elimu Form One Notes Viusasa Elimu Form Three Notes Viusasa Elimu Form Two Viusasa Viusasa Education Viusasa Elimu Viusasa Elimu Class 6 Viusasa Elimu Form 1 Viusasa Elimu Form 1 Notes Viusasa Elimu Form 2 Viusasa Elimu Form 2 Notes Viusasa Elimu Form 3 Viusasa Elimu Form 3 Notes Viusasa Elimu Form 4 Viusasa Elimu Form 4 Notes Viusasa Elimu Form Four Viusasa Elimu Form Four Notes Viusasa Elimu Form One Viusasa Elimu Form One Notes Viusasa Elimu Form Three Viusasa Elimu Form Three Notes Viusasa Elimu Form Two Viusasa Elimu Form Two Notes Viusasa High School Notes - Revision Materials for Kenyan Schools Viusasa Notes Mathematics Mock Papers Mathematics Paper 1 2019 Mathematics Paper 1 Notes Mathematics Paper 1 Questions and Answers Mathematics Paper 1 Questions and Answers Pdf Mathematics Paper 2 Form 3 Mathematics Paper 2 Notes Mathematics Paper 2 Questions and Answers Pdf Mathematics Past Papers Mathematics Past Papers Pdf Mathematics Questions and Answers Pdf Mathematics Revision Questions and Answers Pdf Mathematics Revision Questions Pdf Common Exam Questions in Mathematics Paper 1 Common Exam Questions in Mathematics Paper 2 Common Test Questions in Mathematics Paper 1 Common Tested Questions in Mathematics Paper 1 Commonly Tested Questions in Mathematics Paper 1 K.c.s.e.Mathematics Questions and Answers KCSE 2019 Mathematics Paper 1 Marking Scheme KCSE 2019 Mathematics Paper 2 KCSE 2019 Mathematics Paper 2 Marking Scheme KCSE 2021 Prediction Questions and Answers KCSE Mathematics Paper 1 2019 KCSE Mathematics Paper 2 2016 KCSE Mathematics Paper 2 2017 KCSE Mathematics Paper 2 2018 KCSE Mathematics Paper 2 2019 KCSE Mathematics Questions and Answers Most Tested Questions in Mathematics Paper 1 Most Tested Questions in Mathematics Paper 2 Mostly Tested Questions in Mathematics Paper 1 Mostly Tested Questions in Mathematics Paper 2 A Level Maths Notes Uganda Pdf Download Buddo Junior School Holiday Work Maths Notes for a Level Pdf Maths Notes Form 1 Maths Notes Form 3 the Mole Maths Notes Form 4 Maths Notes O Level Maths Notes O Level Uganda Maths Notes O Level Uganda Pdf Maths Notes Pdf Download Maths Notes Form 3 Maths Notes Form 3 Maths Questions and Answers Form Three Maths Syllabus Pdf Gayaza High School Maths Notes Gayaza High School Maths Notes Pdf Gayaza High School Maths Past Papers Gayaza High School Maths Past Papers Answers Gayaza High School Maths Past Papers Questions and Answers Gayaza High School E Learning Gayaza High School Elearning Platform Gayaza High School Examinations Gayaza High School Holiday Work Gayaza High School Notes Gayaza High School Notes 2022 Gayaza High School Notes 2026 Gayaza High School Notes 2025 Gayaza High School Notes Pdf Gayaza Junior School E Learning Platform Gayaza Junior School Holiday Work Gayaza O Level Maths Notes Home › Gayaza High School | Elearning Platform Kabojja Junior School Holiday Work Pdf Klb Maths Book 3 Klb Maths Form 3 Teachers Guide Klb Maths Notes List of Ugandan E-learning Platforms for Students Mirembe Junior School Holiday Work Ntare School Past Papers O Level Maths Notes Free Download O Level Maths Notes in Uganda O Level Maths Notes Pdf O Level Maths Notes Uganda Pdf O Level Maths Notes Uganda Pdf Download O Level General - Home › Gayaza High School | Elearning S.1 Maths Notes | Standard High School Zzana S.3 Maths Notes S.4 Maths 2 Notes | Standard High School Zzana Seeta High School Elearning Seeta High School Holiday Work Seeta High School Notes Seeta High School Notes Pdf Seeta High School Past Papers Seeta High School Past Papers Pdf Senior 1 Maths Notes Senior 1 Maths Notes in Uganda Senior 1 Maths Notes Uganda Senior 1 Maths Questions Senior 1 Exams Senior 1 Work Senior 1 Work 2021 Senior 1 Work 2021 Uganda Senior 2 Maths Notes Senior 2 Maths Notes in Uganda Senior 2 Maths Notes Uganda Senior 2 Maths Questions Senior 2 Exams Senior 2 Work Senior 2 Work 2021 Senior 2 Work 2021 Uganda Senior 3 Maths Notes Senior 3 Maths Notes in Uganda Senior 3 Maths Notes Uganda Senior 3 Maths Questions Senior 3 Exams Senior 3 Work Senior 3 Work 2021 Senior 3 Work 2021 Uganda Senior 4 Maths Notes Senior 4 Maths Notes in Uganda Senior 4 Maths Notes Uganda Senior 4 Maths Questions Senior 4 Exams Senior 4 Work Senior 4 Work 2021 Senior 4 Work 2021 Uganda Senior Four Maths Notes Senior Four Maths Notes in Uganda Senior Four Maths Notes Uganda Senior Four Maths Questions Senior Four Exams Senior Four Work Senior Four Work 2021 Senior Four Work 2021 Uganda Senior One Maths Notes Senior One Maths Notes in Uganda Senior One Maths Notes Uganda Senior One Maths Questions Senior One Exams Senior One Work Senior One Work 2021 Senior One Work 2021 Uganda Senior Three Maths Notes Senior Three Maths Notes in Uganda Senior Three Maths Notes Uganda Senior Three Maths Questions Senior Three Exams Senior Three Work Senior Three Work 2021 Senior Three Work 2021 Uganda Senior Two Maths Notes Senior Two Maths Notes in Uganda Senior Two Maths Notes Pdf Senior Two Maths Notes Uganda Senior Two Maths Questions Senior Two Exams Senior Two Work Senior Two Work 2021 Senior Two Work 2021 Uganda St Mary's Kitende E Learning Standard High School Notes Standard High School Zana a Level Notes Standard High School Zana Com Notes Standard High School Zana E Learning Standard High School Zana E Learning Platform Standard High School Zana E-learning Platform Standard High School Zana Notes for Senior Two Standard High School Zana Notes Pdf Standard High School Zana Website Standard High Zana Notes Uace Maths Notes Uace Maths Notes Pdf Uce Maths Notes Pdf A Level Mathematics Notes Uganda Pdf Download Buddo Junior School Holiday Work Mathematics Notes for a Level Pdf Mathematics Notes Form 1 Mathematics Notes Form 3 the Mole Mathematics Notes Form 4 Mathematics Notes O Level Mathematics Notes O Level Uganda Mathematics Notes O Level Uganda Pdf Mathematics Notes Pdf Download Mathematics Notes Form 3 Mathematics Notes Form 3 Mathematics Questions and Answers Form Three Mathematics Syllabus Pdf Gayaza High School Mathematics Notes Gayaza High School Mathematics Notes Pdf Gayaza High School Mathematics Past Papers Gayaza High School Mathematics Past Papers Answers Gayaza High School Mathematics Past Papers Questions and Answers Gayaza High School E Learning Gayaza High School Elearning Platform Gayaza High School Examinations Gayaza High School Holiday Work Gayaza High School Notes Gayaza High School Notes 2022 Gayaza High School Notes 2023 Gayaza High School Notes 2024 Gayaza High School Notes Pdf Gayaza Junior School E Learning Platform Gayaza Junior School Holiday Work Gayaza O Level Mathematics Notes Home › Gayaza High School | Elearning Platform Kabojja Junior School Holiday Work Pdf Klb Mathematics Book 3 Klb Mathematics Form 3 Teachers Guide Klb Mathematics Notes List of Ugandan E-learning Platforms for Students Mirembe Junior School Holiday Work Ntare School Past Papers O Level Mathematics Notes Free Download O Level Mathematics Notes in Uganda O Level Mathematics Notes Pdf O Level Mathematics Notes Uganda Pdf O Level Mathematics Notes Uganda Pdf Download O Level General - Home › Gayaza High School | Elearning S.1 Mathematics Notes | Standard High School Zzana S.3 Mathematics Notes S.4 Mathematics 2 Notes | Standard High School Zzana Seeta High School Elearning Seeta High School Holiday Work Seeta High School Notes Seeta High School Notes Pdf Seeta High School Past Papers Seeta High School Past Papers Pdf Senior 1 Mathematics Notes Senior 1 Mathematics Notes in Uganda Senior 1 Mathematics Notes Uganda Senior 1 Mathematics Questions Senior 1 Exams Senior 1 Work Senior 1 Work 2021 Senior 1 Work 2021 Uganda Senior 2 Mathematics Notes Senior 2 Mathematics Notes in Uganda Senior 2 Mathematics Notes Uganda Senior 2 Mathematics Questions Senior 2 Exams Senior 2 Work Senior 2 Work 2021 Senior 2 Work 2021 Uganda Senior 3 Mathematics Notes Senior 3 Mathematics Notes in Uganda Senior 3 Mathematics Notes Uganda Senior 3 Mathematics Questions Senior 3 Exams Senior 3 Work Senior 3 Work 2021 Senior 3 Work 2021 Uganda Senior 4 Mathematics Notes Senior 4 Mathematics Notes in Uganda Senior 4 Mathematics Notes Uganda Senior 4 Mathematics Questions Senior 4 Exams Senior 4 Work Senior 4 Work 2021 Senior 4 Work 2021 Uganda Senior Four Mathematics Notes Senior Four Mathematics Notes in Uganda Senior Four Mathematics Notes Uganda Senior Four Mathematics Questions Senior Four Exams Senior Four Work Senior Four Work 2021 Senior Four Work 2021 Uganda Senior One Mathematics Notes Senior One Mathematics Notes in Uganda Senior One Mathematics Notes Uganda Senior One Mathematics Questions Senior One Exams Senior One Work Senior One Work 2021 Senior One Work 2021 Uganda Senior Three Mathematics Notes Senior Three Mathematics Notes in Uganda Senior Three Mathematics Notes Uganda Senior Three Mathematics Questions Senior Three Exams Senior Three Work Senior Three Work 2021 Senior Three Work 2021 Uganda Senior Two Mathematics Notes Senior Two Mathematics Notes in Uganda Senior Two Mathematics Notes Pdf Senior Two Mathematics Notes Uganda Senior Two Mathematics Questions Senior Two Exams Senior Two Work Senior Two Work 2021 Senior Two Work 2021 Uganda St Mary's Kitende E Learning Standard High School Notes Standard High School Zana a Level Notes Standard High School Zana Com Notes Standard High School Zana E Learning Standard High School Zana E Learning Platform Standard High School Zana E-learning Platform Standard High School Zana Notes for Senior Two Standard High School Zana Notes Pdf Standard High School Zana Website Standard High Zana Notes Uace Mathematics Notes Uace Mathematics Notes Pdf Uce Mathematics Notes Pdf Uce Mathematics Notes Pdf Download Uce Past Papers Uganda Secondary Schools E-learning Platform Uneb Marking Guides Pdf Uneb Past Papers and Answers Pdf Uce Maths Notes Pdf Download Uce Past Papers Uganda Secondary Schools E-learning Platform Uneb Marking Guides Pdf Uneb Past Papers and Answers Pdf Ntare School Past Papers Seeta High School Notes Pdf Seeta High School Past Papers Seeta High School Past Papers Pdf St Mary's Kitende Past Papers Uce Mathematics Notes Pdf Uce Past Papers Uneb Marking Guides Pdf Uneb Past Papers and Answers Pdf Gayaza High School Mathematics Notes Gayaza High School Notes Pdf O Level Mathematics Notes in Uganda O Level Maths Notes Free Download Senior Two Mathematics Notes Pdf Uace Mathematics Notes Uace Mathematics Notes Pdf Uce Math Notes Pdf Uce Math Notes Pdf Download Last Year Kcse Exams for Marths Last Year Kcse Exams for Maths Last Year Kcse Exams for Mathematics Last Year Kcse Past Papers for Marths Last Year Kcse Past Papers for Maths Last Year Kcse Past Papers for Mathematics Download Secondary Mathematics Mock Papers Solving Problems Mathematics Paper 2 Pdf Download Kcse 2021 Mathematics Paper 1 Marking Scheme Kcse 2021 Mathematics Paper 2 Marking Scheme Mathematics Paper 1 Questions and Answers Pdf Kcse Mathematics Questions and Answers Pdf Kcse Mock Papers Pdf 2020 Mathematics Paper 1 Questions and Answers Pdf 2020 Mathematics Paper 2 Questions and Answers Pdf
Scholarship 2026/27
Current Scholarships 2026/2027 - Fully Funded
Full Undergraduate Scholarships 2026 - 2027
Fully Funded Masters Scholarships 2026 - 27
PhD Scholarships for International Students - Fully Funded!
Funding Opportunities for Journalists 2026/2027
Funding for Entrepreneurs 2026/2027
***
